1. INTRODUCTION
1.1 Purpose and Scope
General chapter Design and Development of Biological Assays  1032
1032 presents methodology for the development of bioassay procedures that have sound experimental design, that provide data that can be analyzed using well-founded statistical principles, and that are fit for their specific use.
presents methodology for the development of bioassay procedures that have sound experimental design, that provide data that can be analyzed using well-founded statistical principles, and that are fit for their specific use.
General chapter  1032
1032 is one of a group of five general chapters that focus on relative potency assays, in which the activity of a Test material is quantified by comparison to the activity of a Standard material. However, many of the principles can be applied to other assay systems.
is one of a group of five general chapters that focus on relative potency assays, in which the activity of a Test material is quantified by comparison to the activity of a Standard material. However, many of the principles can be applied to other assay systems.
This general chapter is intended to guide the design and development of a bioassay for a drug substance or product intended for commercial distribution. Although adoption of this chapter's recommended methods may be resource intensive during assay development, early implementation can yield benefits. Lastly, the perspectives and methods described herein are those recommended from among the many alternatives which contemporary bioassay theory and practice offers.
Focus on Relative Potency—
Because of the inherent variability in biological test systems (including that from animals, cells, instruments, reagents, and day-to-day and between-lab), an absolute measure of potency is more variable than a measure of activity relative to a Standard. This has led to the adoption of the relative potency methodology. Assuming that the Standard and Test materials are biologically similar, statistical similarity (a consequence of the Test and Standard similarity) should be present, and the Test sample can be expected to behave like a concentration or dilution of the Standard. Relative potency is a unitless measure obtained from a comparison of the dose-response relationships of Test and Standard drug preparations. For the purpose of the relative comparison of Test to Standard, the potency of the Standard is usually assigned a value of 1 (or 100%). The Standard can be a material established as such by a national (e.g., USP) or international (e.g., WHO) organization, or it could be an internal Standard.
1.2 Audience
This chapter is intended for both the practicing bioassay analyst and the statistician who are engaged in developing a bioassay. The former will find guidance for implementing bioassay structure and methodology to achieve analytical goals while reliably demonstrating the biological activity of interest, and the latter will gain insights regarding the constraints of biology that can prove challenging to balance with a rigorous practice of statistics.
2. BIOASSAY FITNESS FOR USE
To evaluate whether an assay is fit for use, analysts must specify clearly the purpose(s) for performing the bioassay. Common uses for a bioassay include lot release of drug substance (active pharmaceutical ingredient) and drug product; assessment of stability; qualification of Standard and other critical reagents; characterization of process intermediates and formulations; characterization of contaminants and degradation products; and support of changes in the product production process. The relative accuracy, specificity, precision, and robustness requirements may be different for each of these potential uses. It is a good strategy to develop and validate a bioassay to support multiple intended uses; for example, a bioassay primarily developed for batch release may serve other purposes. Decisions about fitness for use are based on scientific and statistical considerations, as well as practical considerations such as cost, turnaround time, and throughput requirements for the assay.
When assays are used for lot release, a linear-model bioassay may allow sufficient assessment of similarity. For bioassays used to support stability, comparability, to qualify reference materials or critical reagents, or in association with changes in the production or assay processes, it is generally useful to assess similarity using the entire concentration–response curve, including the asymptotes (if present).
2.1 Process Development
Bioassays are generally required in the development and optimization of product manufacturing, including formulation and scale-up processes. Bioassays can be used to evaluate purification strategies, optimize product yield, and measure product stability. Because samples taken throughout the process are often analyzed and compared, sample matrix effects that may affect assay response should be carefully studied to determine an assay’s fitness for use. For relative potency measures, the Standard material may require dilution into a suitable matrix for quantitation. The bioassay’s precision and accuracy should be sufficient for measuring process performance or for assessing and comparing the stability of candidate formulations.
2.2 Process Characterization
Bioassays may be performed to assess the effect on drug potency associated with different stages of drug manufacture or with changes in the manufacturing process (e.g., to demonstrate product equivalence before and after process changes are made). Bioassays used in this type of application may be qualitative or quantitative.
2.3 Product Release
Bioassays are used to evaluate the potency of the drug before commercial product release. To the extent possible, the assay should reflect or mimic the product’s known or intended mechanism of action. If the bioassay does not include the functional biology directly associated with the mechanism of action, it may be necessary to demonstrate a relationship between the bioassay’s estimated potency determinations and those of some other assay that better or otherwise reflects putative functional activity.
For product-release testing, product specifications are established to define a minimum or range of potency values that are acceptable for product. The precision of the reportable value from the bioassay must support the number of significant digits listed in the specification (see general chapter Biological Assay Validation  1033
1033 ), and, in conjunction with relative accuracy, support the specification range. In order to meet these specifications, manufacturing quality control will have sufficiently narrow product release specifications in order to accommodate any loss of activity due to instability and uncertainty in the release assay.
), and, in conjunction with relative accuracy, support the specification range. In order to meet these specifications, manufacturing quality control will have sufficiently narrow product release specifications in order to accommodate any loss of activity due to instability and uncertainty in the release assay.
2.4 Process Intermediates
Bioassay assessment of process intermediates can provide information regarding specificity. Formulation and fill strategies may rely on bioassays in order to ensure that drug product, including that in final container, will meet its established specifications. For example, unformulated bulk materials may be held and evaluated for potency. Bulks may be pooled with other bulk lots, diluted, or reworked based on the potency results. For these types of applications, the bioassay must be capable of measuring product activity in different matrices. In some cases, a separate Standard material is made and is used to calculate relative potency for the process intermediate.
2.5 Stability
The potency assay may be used to assess biotechnology and vaccine product stability. Information from stability studies, performed during development under actual and/or accelerated or stressed storage conditions, may be used to establish shelf life duration as well as to identify and estimate degradation products and degradation rates. Post licensure stability studies may be used to monitor product stability. Knowledge of both short-term and long-term variability of the bioassay is important to assure an acceptable level of uncertainty in potency measures obtained.
2.6 Qualification of Reagents
The quantitative characterization of a new Standard requires an accurate and precise measurement of the new Standard’s biological activity. This measurement is used either to establish that the new Standard lot is equivalent to the previous lot or to assign it a label potency to which Test samples can be compared. Additional replication (beyond routine testing) may be required to achieve greater precision in the potency measurement of the new Standard material. Additionally, the bioassay may be used to qualify a cell culture reagent such as fetal bovine serum. The fitness for use in such cases is tied to the ability of the assay to screen reagent lots and to ensure that lots that may bias or compromise the relative potency measurements are not accepted.
2.7 Product Integrity
Biotechnology, biological, and vaccine products may contain a population of heterogeneous material, including the intended predominant product material. Some process impurities and degradation products may be active, partially active, inactive in, or antagonistic to, the response measured in the bioassay. For product variants or derivatives for which changes in structure or relative composition may be associated with subtle yet characteristic changes in the bioassay response (e.g., change in slope or asymptote), the bioassay may be useful in the detection and measurement of these variants or derivatives. Studies that identify characteristic changes associated with variants of the intended product help ensure consistent product performance. Whenever practical, the bioassay should be accompanied by orthogonal methods that are sensitive to product variants, process impurities, and/or degradation products.
3. BIOASSAY FUNDAMENTALS
3.1 In Vivo Bioassays
In vivo potency assays are bioassays in which sets of dilutions of the Standard and Test materials are administered to animals and the concentration–response relationships are used to estimate potency. For some animal assays, the endpoint is simple (e.g., rat body weight gain assay for human growth hormone or rat ovarian weight assay for follicle stimulating hormone), but others require further processing of samples collected from treated animals (e.g., reticulocyte count for erythropoeitin, steroidogenesis for gonadotropins, neutrophil count for granulocyte colony stimulating factor, or antibody titer after administration of vaccines). With the advent of cell lines specific for the putative physiological mechanism of action (MOA), the use of animals for the measurement of potency has substantially diminished. Cost, low throughput, ethical, and other practical issues argue against the use of animal bioassays. Regulatory agencies have encouraged the responsible limitation of animal use whenever possible (see The Interagency Coordinating Committee on the Validation of Alternative Methods, Mission, Vision, and Strategic Priorities; February 2004). When in vitro activity is not strongly associated with in vivo activity (e.g., EPO), the combination of an in vitro cell-based assay and a suitable physicochemical method (e.g., IEF, glycan analysis) may substitute for in vivo assays. However, a need for in vivo assays may remain when in vitro assays cannot detect differences that are critical in regard to a drug's intended biological function.
Animals' physiological responses to biological drugs (including vaccines) may predict patients' responses. Selection of animal test subjects by species, strain, gender, and maturity or weight range is guided by the goal of developing a representative and sensitive model with which to assess the activity of Test samples.
Some assay methods lend themselves to the use of colony versus naive animals. For example, pyrogen and insulin testing benefit from using experienced colony rabbits that provide a reliable response capacity. If animals recently introduced to the colony fail to respond as expected after several administrations of a compound, they should be culled from the colony so they do not cause future invalid or indeterminate assay results. In the case of assaying highly antigenic compounds for pyrogens, however, naive animals should be used to avoid generating inaccurate or confounded results. Other colony advantages include common controlled environmental conditions (macro/room, and micro/rack), consistent feeding schedule, provision of water, and husbandry routine.
Historical data including colony records and assay data can be used to identify factors that influence assay performance. The influence of biasing factors can be reduced by applying randomization principles such as distribution of weight ranges across dose groups, group assignments from shipping containers to different cages, or use of computer-generated or deck patterns for injection/dosing. A test animal must be healthy and have time to stabilize in its environment to be suitable for use in a bioassay. Factors that combine to influence an animal’s state of health include proper nutrition, hydration, freedom from physical and psychological stressors, adequate housing sanitization, controlled light cycle (diurnal/nocturnal), experienced handling, skillful injections and bleedings, and absence of noise or vibration. Daily observation of test animals is essential for maintenance of health, and veterinary care must be available to evaluate issues that have the potential to compromise the validity of bioassay results.
3.2 Ex Vivo Bioassays
Cells or tissues from human or animal donors can be cultured in the laboratory and used to assess the activity of a Test sample. In the case of cytokines, the majority of assays use cells from the hematopoietic system or subsets of hematopoietic cells from peripheral blood such as peripheral blood mononuclear cells or peripheral blood lymphocytes. For proteins that act on solid tissues, such as growth factors and hormones, specific tissue on which they act can be removed from animals, dissociated, and cultured for a limited period either as adherent or semi-adherent cells. Although an ex vivo assay system has the advantage of similarity to the natural milieu, it may also suffer from substantial donor-to-donor variability, as well as challenging availability of appropriate cells.
Bioassays that involve live tissues or cells from an animal (e.g., rat hepatocyte glucagon method) require process management similar to that of in vivo assays to minimize assay variability and bias. The level of effort to manage bias (e.g., via randomization) should be appropriate for the purpose of the assay. Additional factors that may affect assay results include time of day, weight or maturity of animal, anesthetic used, buffer components/reagents, incubation bath temperature and position, and cell viability.
3.3 In Vitro (Cell-Based) Bioassays
Bioassays using cell lines that respond to specific ligands or infectious agents can be used for lot-release assays. These cell lines can be derived from tumors, immortalized as factor-dependent cell lines, or engineered cell lines transfected with appropriate receptors. Additionally, nontransformed cell lines which can be maintained over a sufficient number of passages (e.g., fibroblasts) may also be used. Regardless of cell line, there is an expectation of adequately equivalent potency response through some number of continuous passages. Advances in recombinant DNA technology and the understanding of cellular signaling mechanisms have allowed the generation of engineered cell lines with improved response, stable expression of receptors and signaling mechanisms, and longer stability. The cellular responses to the protein of interest depend on the drug’s MOA and the duration of exposure. Such responses include cell proliferation, cell killing, antiviral activity, differentiation, cytokine/mediator secretion, and enzyme activation. Assays involving these responses may require incubation of the cells over several days, during which time contamination, uneven evaporation, or other location effects may arise. Comparatively rapid responses based on an intracellular signaling mechanism—such as second messengers, protein kinase activation, or reporter gene expression—have proven acceptable to regulatory authorities. Lastly, most cell lines used for bioassays express receptors for multiple cytokines and growth factors. This lack of specificity may not be detrimental if the Test sample's specificity is demonstrated.
Cell-based bioassay design should reflect knowledge of the factors that influence the response of the cells to the active analyte. Response variability is often reflected in parameters such as slope, EC50 of the concentration–response curve, or the response range (maximum minus minimum response). Even though relative potency methodology minimizes the effects on potency estimates of variation in these parameters among assays, and among blocks within an assay, such response variability can make an assay difficult to manage (i.e., it may be difficult to assess system suitability). Hence, while assay development should be focused primarily on the properties of potency, efforts to identify and control variation in the concentration–response relationship are also appropriate. For blocked assays (e.g., multiple cell culture plates in an assay) with appreciable variation in curve shape among blocks, an analysis that does not properly include blocks will yield inflated estimates of within-assay variation, making similarity assessment particularly difficult. Two strategies are available for addressing variation among blocks: one, a laboratory effort to identify and control sources of variation and two, a statistical effort to build and use a blocked design and analysis. Combining these strategies can be particularly effective.
The development of a cell-based bioassay begins with the selection or generation of a cell line. An important first step when developing a cell-based assay to assess a commercial product is to verify that the cell line of interest is not restricted to research use only. To ensure an adequate and consistent supply of cells for product testing, a cell bank should be generated if possible. To the extent possible, information regarding functional and genetic characteristics of the bioassay’s cell line should be documented, including details of the cell line's history from origin to banking. For example, for a recombinant cell line this might include the identification of the source of the parental cell line (internal cell bank, external repository, etc.), of the DNA sequences used for transfection, and of the subsequent selection and functional testing regimen that resulted in selection of the cell line. Ideally, though not always practical, sufficient information is available to permit recreation of a similar cell line if necessary. Pertinent information may include identity (e.g., isoenzyme, phenotypic markers, genetic analysis); morphology (e.g., archived photographic images); purity (e.g., mycoplasma, bacteria, fungus and virus testing); cryopreservation; thaw and culture conditions (e.g., media components, thaw temperature and method, methods of propagation, seeding densities, harvest conditions); thaw viability (immediately after being frozen and after time in storage); growth characteristics (e.g., cell doubling times); and functional stability (e.g., ploidy).
Cell characterization and vigilance regarding aspects of assay performance that reflect on cell status are necessary to ensure the quality and longevity of cell banks for use in the QC environment. The general health and metabolic state of the cells at the time of bioassay can substantially influence the test results. After a cell line has been characterized and is ready for banking, analysts typically prepare a two-tiered bank (Master and Working). A Master Cell Bank is created as the source for the Working Cell Bank. The Working Cell Bank is derived by expansion of one or more vials of the Master Cell Bank. The size of the banks depends on the growth characteristics of the cells, the number of cells required for each assay, and how often the assay will be performed. Some cells may be sensitive to cryopreservation, thawing, and culture conditions, and the banks must be carefully prepared and characterized before being used for validation studies and for regular use in the QC laboratory.
There follow factors that may affect bioassay response and the assessment of potency, that are common to many cell-based bioassays: cell type (adherent or nonadherent); cell thawing; plating density (at thaw and during seed train maintenance) and confluence (adherent cells); culture vessels; growth, staging, and assay media; serum requirements (source, heat inactivation, gamma irradiation); incubation conditions (temperature, CO2, humidity, culture times from thaw); cell harvesting reagents and techniques (for adherent cells, method of dissociation); cell sorting; cell counting; determination of cell health (growth rate, viability, yield); cell passage number and passaging schedule; cell line stability (genetic, receptor, marker, gene expression level); and starvation or stimulation steps. This list is not exhaustive, and analysts with comprehensive understanding and experience with the cell line should be involved during assay development. These experienced individuals should identify factors that might influence assay outcomes and establish strategies for an appropriate level of control whenever possible.
3.4 Standard
The Standard is a critical reagent in bioassays because of the necessity to have a reliable material to which a Test preparation can be quantitatively compared. The Standard may be assigned a unitage or specific activity that represents fully (100%) potent material. Where possible, a Standard should be representative of the samples to be tested in the bioassay. Testing performed to qualify a Standard may be more rigorous than the routine testing used for lot release.
A Standard must be stored under conditions that preserve its full potency for the intended duration of its use. To this end, the Standard may be stored under conditions that are different from the normal storage of the drug substance or drug product. These could include a different temperature (e.g., 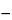 70
70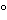 or
or 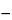 20
20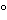 , instead of 2
, instead of 2 –8
–8 ), a different container (e.g., plastic vials instead of syringes), a different formulation (e.g., lyophilizable formulation or the addition of carrier proteins such as human serum albumin, stabilizers, etc.). The Standard material should be tested for stability at appropriate intervals. System suitability criteria of the bioassay such as maximum or background response, EC50 slope, or potency of assay control may be used to detect change in the activity of the Standard. Accelerated stability studies can be performed to estimate degradation rates and establish recognizable characteristics of Standard instability.
), a different container (e.g., plastic vials instead of syringes), a different formulation (e.g., lyophilizable formulation or the addition of carrier proteins such as human serum albumin, stabilizers, etc.). The Standard material should be tested for stability at appropriate intervals. System suitability criteria of the bioassay such as maximum or background response, EC50 slope, or potency of assay control may be used to detect change in the activity of the Standard. Accelerated stability studies can be performed to estimate degradation rates and establish recognizable characteristics of Standard instability.
At later stages in clinical development, the Standard may be prepared using the manufacturing process employed in pivotal clinical trials. If the Standard formulation is different from that used in the drug product process, it is important to demonstrate that the assay’s assessment of similarity and estimate of potency is not sensitive to the differences in formulation. An initial Standard may be referred to as the Primary Standard. Subsequent Standards can be prepared using current manufacturing processes and can be designated Working Standards. Separate SOPs may be required for establishing these standards for each product. Bias in potency measurements sometimes can arise if the activity of the Standard gradually changes. Also, loss of similarity may be observed if, with time, the Standard undergoes changes in glycosylation. It is prudent to archive aliquots of each Standard lot for assessment of comparability with later Standards and for the investigation of assay drift.
4. STATISTICAL ASPECTS OF BIOASSAY FUNDAMENTALS
The statistical elements of bioassay development include the type of data, the measure of response at varying concentration, the assay design, the statistical model, pre-analysis treatment of the data, methods of data analysis, suitability testing, and outlier analysis. These form the constituents of the bioassay system that will be used to estimate the potency of a Test sample.
4.1 Data
Fundamentally, there are two bioassay data types: quantitative and quantal (categorical). Quantitative data can be either continuous (not limited to discrete observations; e.g., collected from an instrument), count (e.g., plaque-forming units), or discrete (e.g., endpoint dilution titers). Quantal data are often dichotomous; for example, life/death in an animal response model or positivity/negativity in a plate-based infectivity assay that results in destruction of a cell monolayer following administration of an infectious agent. Quantitative data can be transformed to quantal data by selecting a threshold that distinguishes a positive response from a negative response. Such a threshold can be calculated from data acquired from a negative control, as by adding (or subtracting) a measure of uncertainty (such as two or three times the standard deviation of negative control responses) to the negative control average. Analysts should be cautious about transforming quantitative data to quantal data because this results in a loss of information.
4.2 Assumptions
A key assumption for the analysis of most bioassays is that the Standard and Test samples contain the same effective analyte or population of analytes and thus may be expected to behave similarly in the bioassay. This is termed similarity. As will be shown in more detail in the general chapter Analysis of Biological Assays  1034
1034 for specific statistical models, biological similarity implies that statistical similarity is present (for parallel-line and parallel-curve models, the Standard and Test curves are parallel; for slope-ratio models, the Standard and Test lines have a common intercept). The reverse is not true. Statistical similarity (parallel lines, parallel curves, or common intercept, as appropriate) does not ensure biological similarity. However, failure to satisfy statistical similarity may be taken as evidence against biological similarity. The existence of a Standard–Test sample pair that passes the assessment of statistical similarity is thus a necessary but not sufficient condition for the satisfaction of the key assumption of biological similarity. Biological similarity thus remains, unavoidably, an assumption. Departures from statistical similarity that are consistent in value across replicate assays may be indicative of matrix effects or of real differences between Test and Standard materials. This is true even if the departure from statistical similarity is sufficiently small to support determination of a relative potency.
for specific statistical models, biological similarity implies that statistical similarity is present (for parallel-line and parallel-curve models, the Standard and Test curves are parallel; for slope-ratio models, the Standard and Test lines have a common intercept). The reverse is not true. Statistical similarity (parallel lines, parallel curves, or common intercept, as appropriate) does not ensure biological similarity. However, failure to satisfy statistical similarity may be taken as evidence against biological similarity. The existence of a Standard–Test sample pair that passes the assessment of statistical similarity is thus a necessary but not sufficient condition for the satisfaction of the key assumption of biological similarity. Biological similarity thus remains, unavoidably, an assumption. Departures from statistical similarity that are consistent in value across replicate assays may be indicative of matrix effects or of real differences between Test and Standard materials. This is true even if the departure from statistical similarity is sufficiently small to support determination of a relative potency.
In many assays multiple compounds will yield similar concentration–response curves. It may be reasonable to use a biological assay system to describe or even compare response curves from different compounds. But it is not appropriate to report relative potency unless the Standard and Test samples contain only the same active analyte or population of analytes. Biological products typically exhibit lot-to-lot variation in the distribution of analytes (i.e., most biological products contain an intended product and, at acceptably low levels, some process contaminants that may be active in the bioassay). Assessment of similarity is then, at least partially, an assessment of whether the distribution of analytes in the Test sample is close enough to that of the distribution in the Standard sample for relative potency to be meaningful; that is, the assay is a comparison of like to like. When there is evidence (from methods other than the bioassay) that the Standard and Test samples do not contain the same active compound(s), the assumption of biological similarity is not satisfied, and it is not appropriate to report relative potency.
Other common statistical assumptions in the analysis of quantitative bioassays are constant variance of the responses around the fitted model (see section 4.3 Variance Heterogeneity, Weighting, and Transformation for further discussion), normally distributed residuals (a residual is the difference between an observed response and the response predicted by the model), and independence of the residuals.
Constant variance, normality, and independence are interrelated in the practice of bioassay. For bioassays with a quantitative response, a well-chosen data transformation may be used to obtain approximately constant variance and a nearly normal distribution of residuals. Once such transformation has been imposed, the remaining assumption of independence then remains to be addressed via reflection of the assay design structure in the analysis model. Independence of residuals is important for assessing system and sample suitability.
4.3 Variance Heterogeneity, Weighting, and Transformation
Simple analysis of quantitative bioassay data requires that the data be approximately normally distributed with near constant variance across the range of the data. For linear and nonlinear regression models, the variance referred to here is the residual variance from the fit of the model. Constant variance is often not observed; variance heterogeneity may manifest as an increase in variability with increase in response. If the variances are not equal but the data are analyzed as though they are, the estimate of relative potency may still be reasonable; however, failure to address nonconstant variance around the fitted concentration–response model results in an unreliable estimate of within-assay variance. Further, the assessment of statistical similarity may not be accurate, and standard errors and confidence intervals for all parameters (including a Fieller’s Theorem-based interval for the relative potency) should not be used. Confidence intervals for relative potency that combine potency estimates from multiple assays may be erroneous if within-assay error is used for confidence interval calculation.
Constancy of variance may be assessed by means of residual plots, Box-Cox (or power law) analysis, or Levene’s test. With Levene’s test, rather than relying on the p value, change in the statistic obtained is useful as a basis for judging whether homogeneity is improved or worsened. Variance is best assessed on a large body of assay data. Using only the variance among replicates from the current assay is not appropriate, because there are too few data to properly determine truly representative variances specific to each concentration. Data on variance is sparse during development; it is prudent to re-assess variance during validation and to monitor it periodically during ongoing use of the assay.
Two methods used to mitigate variance heterogeneity are transformation and weighting. Lack of constant variance can be addressed with a suitable transformation. Additionally, transformation can improve the normality of residuals and the fit of some statistical models to the data. A transformation should be chosen for an assay system during development, checked during validation, used consistently in routine assay practice, and checked periodically. Bioassay data are commonly displayed with log-transformed concentration; slope-ratio assays are displayed with concentration on the original scale.
Transformation may be performed to the response data as well as to the concentration data. Common choices for a transformation of the response include log, square root (for counts), reciprocal, and, for count data with known asymptotes, logit of the percent of maximum response. Log transformations are commonly used, as they may make nearly linear a useful segment of the concentration–response relationship, and because of the ease of transforming back to the original scale for interpretation. A log–log fit may be performed on data exhibiting nonlinear behavior. Other alternatives are available; i.e., data may be transformed by the inverse of the Power of the Mean (POM) function. A POM coefficient of k = 2 corresponds to a log transformation of the data. For further discussion of relationships between log-transformed and untransformed data, see Appendix in the general chapter Biological Assay Validation 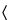 1033
1033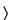 .
.
Note that transformation of the data requires re-evaluation of the model used to fit the data. From a statistical perspective there is nothing special about the original scale of measurement; any transformation that improves accordance with assumptions is acceptable. Analysts should recognize, however, that transformations, choice of statistical model, and choice of weighting scheme are interrelated. If a transformation is used, that may affect the choice of model. That is, transforming the response by a log or square root, for example, may change the shape of the response curve, and, for a linear model, may change the range of concentrations for which the responses are nearly straight and nearly parallel.
For assays with non-constant variance, a weighted analysis may be a reasonable option. Though weighting cannot address lack of residual normality, it is a valid statistical approach to placing emphasis on more precise data. Ideally, weights may be based on the inverse of the predicted within-assay (or within-block) variance of each response where the predictors of variance are independent of responses observed in a specific assay.
In practice, many bioassays have relatively large variation in log EC50 (compared to the variation in log relative potency) among assays (and sometimes among blocks within assay). If not addressed in the variance model, this variation in log EC50 induces what appears to be large variation in response near the mean log EC50, often yielding too-low weights for observations near the EC50.
If the assay is fairly stable (low variability in EC50), an alternative is to look at variance as a function of concentration. While not ideal, an approach using concentration-dependent variances may be reasonable when the weights are estimated from a large number of assays, the variances are small, any imbalance in the number of observations across concentrations is addressed in the variance model, and there are no unusual observations (outliers). This possibility can be examined by plotting the response variance at each concentration (preferably pooled across multiple assays) against concentration and then against a function of concentration (e.g., concentration squared). Variance will be proportional to the function of concentration where this plot approximates a straight line. The apparent slope of this line is informative, in that a horizontal line indicates no weighting is needed. If a function that yields a linear plot can be found, then the weights are taken as proportional to the reciprocal of that function. There may be no such function, particularly if the variation is higher (or lower) at both extremes of the concentration range studied.
Whether a model or historical data are used, the goal is to capture the relative variability at each concentration. It is not necessary to assume that the absolute level of variability of the current assay is identical to that of the data used to determine the weighting, but only that the ratios of variances among concentrations are consistent with the historical data or the data used to determine the variance function.
Appropriate training and experience in statistical methods are essential in determining an appropriate variance-modeling strategy. Sources of variability may be misidentified if the wrong variance model is used. For example, data may have constant variation throughout a four-parameter logistic concentration–response curve but can also have appreciable variation in the EC50 parameter from block to block within the assay, or from assay to assay. If the between-block or between-assay variability is not recognized, this assay can appear to have large variation in the response for concentrations near the long-term average value of the EC50. A weighted model with low weights for concentrations near the EC50 would misrepresent a major feature of such an assay system.
4.4 Normality
Many statistical methods for the analysis of quantitative responses assume normality of the residuals. If the normality assumption is not met, the estimate of relative potency and its standard error may be reasonable, but suitability tests and a confidence interval for the relative potency estimate may be invalid. Most methods used in this chapter are reasonably robust to departures from normality, so the goal is to detect substantial nonnormality. During assay development, in order to discover substantial departure from normality, graphical tools such as a normal probability plot or a histogram (or something similar like stem-and-leaf or box plots) of the residuals from the model fit may be used. The histogram should appear unimodal and symmetric. The normal probability plot should approximate a straight line; a normal probability plot that is not straight (e.g., curved at one end, both ends, or in the middle) indicates the presence of nonnormality. A pattern about a straight line is an indication of nonnormality. Nonnormal behavior may be due to measurements that are log normal and show greater variability at higher levels of response. This may be seen as a concave pattern in the residuals in a normal plot.
Statistical tests of normality may not be useful. As per the previous discussion of statistical testing of constancy of variance, change of the value of a normality test statistic, rather than reliance on a p value, is useful for judging whether normality is improved or worsened. As for variance assessment, evaluate normality on as large a body of assay data as possible during development, re-assess during validation, and monitor periodically during ongoing use of the assay. Important departures from normality can often be mitigated with a suitable transformation. Failure to assess and mitigate important departure from normality carries the risks of disabling appropriate outlier detection and losing capacity to obtain reliable estimates of variation.
4.5 Linearity of Concentration–Response Data
Some bioassay analyses assume that the shape of the concentration–response curve is a straight line or approximates a straight line over a limited range of concentrations. In those cases, a linear-response model may be assessed to determine if it is justified for the data in hand. Difference testing methods for assessing linearity face the same problems as do difference testing methods applied to parallelism—more data and better precision make it more likely to detect nonlinearity. Because instances in which lack of linearity does not affect the potency estimate are rare, analysts should routinely assess departure from linearity if they wish to use a linear-response model to estimate potency.
If an examination of a data plot clearly reveals departure from linearity, this is sufficient to support a conclusion that linearity is not present. High data variability, however, may mask departure from linearity. Thus a general approach for linearity can conform to that for similarity, developed more elaborately in section 4.7 Suitability Testing, Implementing Equivalence Testing for Similarity (parallelism).
- Specify a measure of departure from linearity which can either combine across samples or be sample specific. Possibilities include the nonlinearity sum of squares or quadratic coefficients.
- Use one of the four approaches in Step 2 of Implementing Equivalence Testing for Similarity (parallelism) to determine, during development, a range of acceptable values (acceptance interval) for the measure of nonlinearity.
- Determine a 90% two-sided confidence interval on the measure on nonlinearity, following the Two One-Sided Test (TOST) procedure, and compare the result to the acceptance interval as determined in (2).
Often a subset of the concentrations measured in the assay will be selected in order to establish a linear concentration–response curve. The subset may be identified graphically. The concentrations at the extreme ends of the range should be examined carefully as these often have a large impact on the slope and calculations derived from the slope. If, in the final assay, the intent is to use only concentrations in the linear range, choose a range of concentrations that will yield parallel straight lines for the relative potencies expected during routine use of the assay; otherwise, the assay will fail parallelism tests when the potency produces assay response values outside the linear range of response. When potency is outside the linear range, it may be appropriate to adjust the sample concentration based on this estimated potency and test again in order to obtain a valid potency result. The repeat assays together with the valid assays may generate a biased estimate of potency because of the selective process of repeating assays when the response is in the extremes of the concentration–response curve.
The problem is more complex in assays where there is even modest variation in the shape or location of the concentration–response curve from run to run or from block to block within an assay. In such assays it may be appropriate to choose subsets for each sample in each assay or even in each block within an assay. Note that a fixed-effects model will mask any need for different subsets in different blocks, but a mixed-effects model may reveal and accommodate different subsets in different blocks (see section 4.9 Fixed and Random Effects in Models of Bioassay Response).
Additional guidance about selection of data subset(s) for linear model estimation of relative potency includes the following: use at least three, and preferably four, adjacent concentrations; require that the slope of the linear segment is sufficiently steep; require that the lines fit to Standard and Test samples are straight; and require that the fit regression lines are parallel. One way to derive a steepness criterion is to compute a t-statistic on the slope difference from zero. If the slope is not significant the bioassay is likely to have poor performance; this may be observed as increased variation in the potency results. Another aspect that supports requiring adequate steepness of slope is the use of subset selection algorithms. Without a slope steepness criterion, a subset selection algorithm that seeks to identify subsets of three or more contiguous data points that are straight and parallel might select concentrations on an asymptote. Such subsets are obviously inappropriate to use for potency estimation. How steep or how significant the steepness of the slope should be depends on the assay. This criterion should be set during assay development and possibly refined during assay validation.
4.6 Common Bioassay Models
Most bioassays consist of a series of concentrations or dilutions of both a Test sample and a Standard material. A mathematical model is fit to the concentration–response data, and a relative potency may then be calculated from the parameters of the model. Choice of model may depend on whether quantitative or qualitative data are being analyzed.
For quantitative data, models using parallel response profiles which support comparative evaluation for determining relative potency may provide statistical advantages. If such a model is used, concentrations or dilutions are usually scaled geometrically, e.g., usually in two-fold, log, or half-log increments. If a slope-ratio model is used, concentrations or dilutions can be equally spaced on concentration, rather than log concentration. Several functions may be used for fitting a parallel response model to quantitative data, including a linear function, a higher-order polynomial function, a four-parameter logistic (symmetric sigmoid) function, and a five-parameter logistic function for asymmetric sigmoids. Such functions require a sufficient number of concentrations or dilutions to fit the model. To assess lack of fit of any model it is necessary to have at least one, and preferably several, more concentrations (or dilutions) than the number of parameters that will be estimated in the model. Also, at least one, and better, two, concentrations are commonly used to support each asymptote.
A linear model is sometimes selected because of apparent efficiency and ease of processing. Because bioassay response profiles are usually nonlinear, the laboratory might perform an experiment with a wide range of concentrations in order to identify the approximately linear region of the concentration–response profile. For data that follow a four-parameter logistic model, these are the concentrations near the center of the response region, often from 20% to 80% response when the data are rescaled to the asymptotes. Caution is appropriate in using a linear model because for a variety of reasons the apparently linear region may shift. A stable linear region may be identified after sufficient experience with the assay and with the variety of samples that are expected to be tested in the assay. Data following the four-parameter logistic function may also be linearized by transformation. The lower region of the function is approximately linear when the data are log transformed (log–log fit).
Quantal data are typically fit using more complex mathematical models. A probit or logit model may be used to estimate a percentile of the response curve (usually the 50th percentile) or, more directly, the relative potency of the Test to the Standard. Spearman-Kärber analysis is a non-modeling method that may be employed for determining the 50th percentile of a quantal concentration–response curve.
4.7 Suitability Testing
System suitability and sample suitability assessment should be performed to ensure the quality of bioassay results. System suitability in bioassay, as in other analytical methods, consists of pre-specified criteria by which the validity of an assay (or, perhaps, a run containing several assays) is assessed. Analysts may assess system suitability by determining that some of the parameters of the Standard response are in their usual ranges and that some properties (e.g., residual variation) of the data are in their usual range. To achieve high assay acceptance rates, it is advisable to accept large fractions of these usual ranges (99% or more) and to assess system suitability using only a few uncorrelated Standard response parameters. The choice of system suitability parameters and their ranges may also be informed by empirical or simulation studies that measure the influence of changes in a parameter on potency estimation.
Sample suitability in bioassay is evaluated using pre-specified criteria for the validity of the potency estimate of an individual Test sample, and usually focuses on similarity assessment. System and sample suitability criteria should be established during bioassay development and before bioassay validation. Where there is limited experience with the bioassay, these criteria may be considered provisional.
System Suitability—
System suitability parameters may be selected based on the design and the statistical model. Regardless of the design and model, however, system suitability parameters should be directly related to the quality of the bioassay. These parameters are generally based on standard and control samples. In parallel-line assays, for example, low values of the Standard slope typically yield estimates of potency with low precision. Rather than reject assays with low slope, analysts may find it more effective to use additional replicate assays until the assay system can be improved to consistently yield higher-precision estimates of potency. It may be particularly relevant to monitor the range of response levels and location of asymptotes associated with controls or Standard sample to establish appropriate levels of response. A drift or a trend in some of the criteria may indicate the degradation of a critical reagent or Standard material. Statistical process control (SPC) methods should be implemented to detect trends in system suitability parameters.
Two common measures of system suitability are assessment of the adequacy of the model (goodness of fit) and of precision. With replicates in a completely randomized design, a pure error term may be separated from the assessment of lack of fit. Care should be taken in deriving a criterion for lack of fit; the use of the wrong error term may result in an artificial assessment. The lack of fit sum of squares from the model fit to the Standard may, depending on the concentrations used and the way in which the data differ from the model, be a useful measure of model adequacy. A threshold may be established, based on sensitivity analysis (assessment of assay sensitivity to changes in the analyte) and/or historical data, beyond which the lack of fit value indicates that the data are not suitable. Note that the Test data are not used here; adequacy of the model for the Test is part of sample suitability.
For assessment of precision, two alternatives may be considered. One approach uses the mean squared error (residual variance) from the model fit to the Standard alone. Because this approach may have few degrees of freedom for the variance estimate, it may be more useful to use a pooled mean squared error from separate model fits to Standard and Test. Once the measure is selected, use historical data and sensitivity analysis to determine a threshold for acceptance.
Sample Suitability—
Sample suitability in bioassay generally consists of the assessment of similarity, which can only be done within the assay range. Relative potency may be reported only from samples that both show similarity to Standard, exhibit requisite quality of model fit, and have been diluted to yield an EC50 (and potency) within the range of the assay system.
Similarity—
In the context of similarity assessment, classical hypothesis (difference) testing evaluates a null hypothesis that a measure (a nonsimilarity parameter measuring the difference between Standard and Test concentration–response curves) is zero, with an implicit alternative hypothesis that the measure is non-zero or the statistical assumptions are not satisfied. The usual (“difference test”) criterion that the p-value must be larger than a certain critical value in order to declare the sample similar to reference controls the probability that samples are falsely declared nonsimilar; this is the producer's risk of failing good samples. The consumer’s risk (the risk that nonsimilar samples are declared similar) is controlled via the precision in the nonsimilarity measure and amount of replication in the assay; typically these are poorly assessed, leaving consumer risk uncontrolled.
In contrast to difference testing, equivalence testing for similarity (assessing whether a 90% confidence interval for a measure of nonsimilarity is contained within specified equivalence bounds) allows only a 5% probability that samples with nonsimilarity measures outside the equivalence boundaries will be declared similar (controlling the consumer's risk). With equivalence testing it is practical to examine and manage the producer’s risk by ensuring that there is enough replication in the assay to have good precision in estimating the nonsimilarity measure(s).
For the comparison of slopes, difference tests have traditionally been used to establish parallelism between a Test sample and the Standard sample. Using this approach the laboratory cannot conclude that the slopes are equal. The data may be too variable, or the assay design may be too weak to establish a difference. The laboratory can, however, conclude that the slopes are sufficiently similar using the equivalence testing approach.
Equivalence testing has practical advantages compared to difference testing, including that increased replication yielding improved assay precision will increase the chances that samples will pass the similarity criteria; that decreased assay replication or precision will decrease the chances that samples will pass the similarity criteria; and that sound approaches to combining data from multiple assays of the same sample to better understand whether a sample is truly similar to Standard or not are obtained.
Because of the advantages associated with the use of equivalence testing in the assessment of similarity, analysts may transition existing assays to equivalence testing or may implement equivalence testing methods when changes are made to existing assays. In this effort, it is informative to examine the risk that the assay will fail good samples. This risk depends on the precision of the assay system, the replication strategy in the assay system, and the critical values of the similarity parameters (this constitutes a process capability analysis). One approach to transitioning an established assay from difference testing to equivalence testing (for similarity) is to use the process capability of the assay to set critical values for similarity parameters. This approach is reasonable for an established assay because the risks (of falsely declaring samples similar and falsely declaring samples nonsimilar) are implicitly acceptable, given the assay’s history of successful use.
Similarity measures may be based on the parameters of the concentration–response curve and may include the slope for a straight parallel-line assay; intercept for a slope-ratio assay; the slope and asymptotes for a four-parameter logistic parallel-line assay; or the slope, asymptotes, and nonsymmetry parameter in a five-parameter sigmoid model. In some cases, these similarity measures have interpretable, practical meaning in the assay; certain changes in curve shape, for example, may be associated with specific changes (e.g., the presence of a specific active contaminant) in the product. When possible, discussion of these changes and their likely effects is a valuable part of setting appropriate equivalence boundaries.
Implementing Equivalence Testing for Similarity (parallelism)—
As previously stated, many statistical procedures for assessing similarity are based on a null hypothesis stating that similarity is present and the alternative hypothesis of there being a state of nonsimilarity. Failure to find that similarity is statistically improbable is then taken as a conclusion of similarity. In fact, however, this failure to establish a probabilistic basis for nonsimilarity does not prove similarity. Equivalence testing provides a method for the analyst to proceed to a conclusion (if warranted by the data) of sufficiently similar while controlling the risk of doing so inappropriately. The following provides a sequence for this process of implementing equivalence testing.
Step 1: Choose a measure of nonsimilarity.
Step 2: Specify a range of acceptable values, typically termed an equivalence interval or “indifference zone,” for the measure of nonsimilarity.
Step 3. Examine whether the value of the nonsimilarity measure is found within the equivalence interval of acceptable values.
Step 1: Choose a measure of nonsimilarity.
For the parallel-line case, this could be the difference or ratio of slopes. (The ratio of slopes can be less sensitive to the value of the slope. Framing the slope difference as a proportional change from Standard rather than in absolute slope units has an advantage because it is invariant to the units on the concentration and response axes.) For a slope-ratio assay, the measure of nonsimilarity can be the difference in y-intercepts between Test and Standard samples. Again, it can be advantageous to frame this difference as a proportion of the (possibly transformed) response range of Standard to make the measure invariant to the units of the response.
The determination of similarity could be based on the individual parameters, one at a time; for the four-parameter logistic model, similarity between Standard and Test samples can be assessed discretely for the upper asymptote, the slope, and the lower asymptote. If sigmoid curves with additional parameters are used to fit bioassay data, it is also important to consider addressing similarity between Standard and Test preparations of the additional curve parameters (e.g., asymmetry parameter of the five-parameter model). Alternatively, evaluation of similarity can be based on a single composite measure of nonparallelism, such as the parallelism sum of squares. This is found as the difference in residual sum of squared errors (RSSE) between the value obtained from fitting the Standard and Test curves separately and the value obtained from imposing parallelism:
Parallelism sum of squares = RSSEp 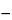 RSSEs
RSSEs 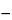 RSSEt
RSSEt
where the subscripts P, S, and T denote Parallel model, Standard model, and Test model, respectively. With any composite measure, the analyst must consider the implicit relative weighting of the importance of the three (or more) curve regions and whether the weighting is appropriate for the problem at hand. For the parallelism sum of squares, for example, with nonlinear models, the weighting given to the comparison of the asymptotes depends on the amount of data in the current assay on and near the asymptotes.
Step 2: Specify a range of acceptable values, typically termed an equivalence interval or “indifference zone,” for the measure of nonsimilarity.
The challenge in implementing equivalence testing is in setting appropriate equivalence bounds for the nonsimilarity measures. Ideally, information is available to link variation in similarity measures to meaningful differences in biological function (as measured by the bioassay). Information may be available from evaluation of orthogonal assays. The following four approaches can be used to determine this interval. If pharmacopeial limits have been specified for a defined measure of nonsimilarity, then the assay should satisfy those requirements.
- The first approach is to compile historical data that compare the Standard to itself and using these data to determine the equivalence interval as a tolerance interval for the measure of nonparallelism. The advantage of using historical data is that they give the laboratory control of the false failure rate (the rate of failing a sample that is in fact acceptable). The disadvantage is that there is no control of the false pass rate (the rate of passing a sample that may have an unacceptable difference in performance relative to the Standard). The equivalence interval specification developed in this way is based solely on assay capability. Laboratories that use this approach should take caution that an imprecise assay in need of improvement may yield such a wide equivalence interval that no useful discrimination of nonsimilarity is possible.
-
Approach (a) is simple to implement in routine use and can be used with assay designs that do not provide reliable estimates of within-assay variation and hence confidence intervals. However, there is a risk that assays with larger than usual amounts of within-assay variation can pass inappropriately. The preferable alternative to (a) is therefore to determine a tolerance interval for the confidence interval for the measure of nonparallelism. The following is particularly appropriate to transition an existing assay with a substantial body of historical data on both Standard and Test samples from a difference testing approach to an equivalence approach:
- For each value of the measure of nonparallelism from the historical data, determine a 95% confidence interval, (m,n).
- For each confidence interval, determine its maximum departure from perfect parallelism. This is max(|m|, |n|) for differences, max(1/m,n) for ratios, and simply n for quantities that must be positive, such as a sum of squares.
- Determine a tolerance interval for the maximum departures obtained in (ii). This will be a one-sided tolerance interval for these necessarily positive quantities. A nonparametric tolerance interval approach is preferred.
- “Sufficiently parallel” is concluded for new data if the confidence interval for the measure of nonparallelism falls completely within the interval determined in (iii).
Approaches (a) and (b), through their reliance on assay capability, control only the false fail rate, and neglect the false pass rate. Incorporating information from sources other than the evaluation of assay capability provides control of the false pass rate. Approaches (c) and (d) are means to this end. - The third approach starts with historical data comparing the Standard to itself and adds data comparing the Standard to known failures, e.g., to degraded samples. Compare values of the measure of nonsimilarity for data for which a conclusion of similarity is appropriate (Standard against itself) and data for which a conclusion of similarity is not appropriate, e.g., degraded samples. Based on this comparison, determine a value of the measure of nonsimilarity that discriminates between the two cases. If this approach is employed, a range of samples for which a conclusion of similarity is not appropriate should be utilized, including samples with the minimal important nonsimilarity. For nonlinear models, this comparison also can be used to determine which parameters should be assessed; some may not be sensitive to the failures that can occur with the specific assay or collection of nonsimilar samples.
- The fourth approach is based on combining a sensitivity analysis of the assay curve to nonsimilarity parameters with what is known about the product and the assay. It is particularly helpful if information is available that links a shift in one or more nonsimilarity measures to properties of the product. These measures may be direct (e.g., conformational changes in a protein) or indirect (e.g., changes in efficacy or safety in an animal model). A complementary approach is provided by a limited sensitivity analysis that combines analyst and biologist judgment regarding the magnitude of shifts in a nonsimilarity parameter that are meaningful, with simulation and/or laboratory experiments, to demonstrate thresholds for similarity parameters that provide protection against important nonsimilarity. Additionally, risk analysis may be informed by the therapeutic index of the drug.
Step 3. Examine whether the value of the nonsimilarity measure is found within the equivalence interval of acceptable values.
For approaches (a) and (b), compare the obtained value of the measure of nonparallelism (a) or its confidence interval (b) to the interval obtained at the beginning of Step 2. The value must be within the limits if one uses (a), or the confidence interval must be completely within the limits if one uses (b).
An alternative to the approach described above [for (a)] is to use an average (historical) value for the variance of the ratio or difference in a similarity parameter—obtained from some number of individual assays—to compute an acceptance interval for a point estimate of the similarity parameter. This approach is simpler to implement in routine use and can be used with assay designs that are unable to provide reliable estimates of within-assay variation. However, there is a price. The equivalence testing approach that relies on assay-specific (within-assay) measure(s) of variation (i.e., the confidence intervals) is conservative in the sense that it will fail to pass similarity for samples from assays that have larger than usual amounts of within-assay variation. Using an acceptance region for a similarity parameter—rather than an acceptance region for confidence intervals for the similarity parameter—loses this conservative property and hence is not preferred where alternatives exist.
For approach (c), an approach that essentially treats the parallelism as a discrimination problem may be used. The choice of the cut point in (c) should take into account the rates of false positive and false negative decisions (and the acceptable risks to the laboratory) and should reflect the between-assay variability in precision. Thus it is reasonable to compare the point estimate of the measure of nonparallelism to the cut point and to not use confidence intervals. This approach is simpler to implement in routine use and can be used with assay designs that cannot provide reliable estimates of within-assay variation.
For approach (d), demonstrate that the measure of nonsimilarity is significantly greater than the lower endpoint of the acceptance interval and significantly less than the upper endpoint. (If the acceptance interval is one-sided, then apply only the single applicable test.) This is use of the TOST approach. For most situations, TOST can be most simply implemented by calculating a 90% two-sided confidence interval, which corresponds to a 5% equivalence test. If this confidence interval lies entirely within the equivalence interval specified at the beginning of Step 2, then similarity is sufficiently demonstrated. For parallel-line models, one can use either (1) a confidence interval based on the value of the difference of the slopes ±k times the standard error of that value, or (2) Fieller's Theorem for the ratio of slopes may be used. For slope ratio models use the confidence interval for the difference of intercepts. For nonlinear models, there is evidence that these simple confidence interval methods do not attain the stated level of confidence, and methods based on likelihood profile or resampling are more appropriate.
Range—
The range for a relative potency bioassay is the interval between the upper and lower relative potencies for which the bioassay is shown to have suitable levels of precision, relative accuracy, linearity of log potency, and success rates for system and sample suitability. It is straightforward to determine whether or not a sample that is similar to a Standard has a relative potency within the (validated) range of the assay system. For samples that are not similar according to established criteria, it is more challenging to determine whether a relative potency estimate for the sample might be obtained. In a nonlinear parallel-line assay a sample that does not have data on one asymptote might be assumed to be out of the potency range of the assay. In a parallel straight-line assay a sample that does not have three or more points on the steep portion of the response curve may be out of the potency range of the assay. For samples that have not been shown to be similar to reference it is not appropriate to report potency or to construct a ratio of EC50s from unrestricted fits. As such samples may be out of the assay range, it may be useful to shift the dilution of the test sample for a subsequent assay on the basis of an estimate of relative activity. This estimated relative activity may be obtained via the ratio of the concentrations of Standard and Test that yields responses that match the reference response at the reference EC50.
4.8 Outliers
Bioassay data should be screened for outliers before relative potency analysis. Outliers may be simple random events or a signal of a systematic problem in the bioassay. Systematic error that generates outliers may be due to a dilution error at one or more concentrations of a Test sample or the Standard or due to a mechanical error (e.g., system malfunction). Several approaches for outlier detection can be considered. Visual inspection is frequently utilized but should be augmented with a more objective approach to avoid potential bias.
An outlier is a datum that appears not to belong among the other data present. An outlier may have a distinct, identifiable cause, such as a mistake in the bench work, equipment malfunction, or a data recording error, or it could just be an unusual value relative to the variability typically seen and may appear without an identifiable cause. The essential question pertaining to an outlier becomes: Is the apparent outlier sampled from the same population as the other, less discordant, data, or is it from another population? If it comes from the same population and the datum is, therefore, an unusual (yet still legitimate) value obtained by chance, then the datum should stand. If it comes from another population and the datum’s excursive value is due to human error or instrument malfunction, then the datum should be omitted from calculations. In practice, the answer to this essential question is often unknown, and investigations into causes are often inconclusive. Outlier management relies on procedures and practices to yield the best answer possible to that essential question and to guide response accordingly.
General chapter Analytical Data—Interpretation and Treatment  1010
1010 addresses outlier labeling, identification, and rejection; statistical methods are included. General chapter
addresses outlier labeling, identification, and rejection; statistical methods are included. General chapter  1010
1010 also lists additional sources of information that can provide a comprehensive review of the relevant statistical methodology. General chapter
also lists additional sources of information that can provide a comprehensive review of the relevant statistical methodology. General chapter  1010
1010 makes no explicit remarks regarding outlier analysis in linear or nonlinear regression. Outlier analysis techniques appropriate for data obtained from regression of response on concentration can be used. Some remarks about outliers are provided here in the context of bioassays to emphasize or complement the information in
makes no explicit remarks regarding outlier analysis in linear or nonlinear regression. Outlier analysis techniques appropriate for data obtained from regression of response on concentration can be used. Some remarks about outliers are provided here in the context of bioassays to emphasize or complement the information in  1010
1010 .
.
Of the procedures employed for analysis of drug compounds and biological drugs, the bioassay may be expected to be the most prone to outlying data. The management of outliers is appropriate with bioassay data on at least two levels: where an individual datum or a group of data (e.g., data at a concentration) can be checked against expected responses for the sample and concentration; and, separately, when estimates of relative potency from an assay can be checked for consistency with other independent estimates of the potency of the same material.
Three important aspects of outlier management are prevention, labeling, and identification.
Outlier prevention is preferred for obvious reasons, and is facilitated by procedures that are less subject to error and by checks that are sensitive to the sorts of errors that, given the experience gained in assay development, may be expected to occur. In effect, the error never becomes an outlier because it is prevented from occurring.
Good practice calls for the examination of data for outliers and labeling (“flagging”) of the apparently outlying observation(s) for investigation. If investigation finds a cause, then the outlying datum may be excluded from analysis. Because of the ordinary occurrence of substantial variability in bioassay response, a laboratory's investigation into the outlying observation is likely to yield no determinable cause. However, the lack of evidence regarding an outlier’s cause is not a clear indication that statistical outlier testing is warranted. Knowledge of the typical range of assay response variability should be the justification for the use of statistical outlier tests.
Outlier identification is the use of rules to confirm that the values are inconsistent with the known or assumed statistical model. For outliers with no determined cause, it is tempting to use statistical outlier identification procedures to discard unusual values. Discarding data solely because of statistical considerations should be a rare event. Falsely discarding data leads to overly optimistic estimates of variability and can bias potency estimates. The laboratory should monitor the failure rate for its outlier procedure and should take action when this is significantly higher than expected.
Statistical procedures for outlier identification depend on assumptions about the distribution of the data without outliers. Identification of data as outliers may mean only that the assumption about distribution is not correct. If dropping outliers because of statistical considerations is common, particularly if outliers tend to occur more often at high values or at high responses, then this may be an indication that the data require some adjustment, such as log transformation, as part of the assay procedure. Two approaches to statistical assessment of outlying data are replication-based and model-based.
Replication-Based Approaches—
When replicates are performed at concentrations of a Test sample and the Standard, an “extra variability” (EV) criterion may be employed to detect outliers. Historical data can be analyzed to determine the range in variability commonly observed among replicates, and this distribution of ranges can be used to establish an extreme in the range that might signal an outlier. Metrics that can be utilized are the simple range (maximum replicate minus minimum replicate), the standard deviation, or the CV or RSD among replicates. However, if the bioassay exhibits heterogeneity of variability, assumptions about uniform scatter of data are unsupported. Analysts can use a variable criterion across levels in the bioassay, or they can perform a transformation of the data to a scale that yields homogeneity of variability. Transformation can be performed with a POM approach as discussed previously. Where heterogeneity exists nonnormality is likely present, and the range rather than standard deviation or RSD should be used.
The actions taken upon detection of a potential outlier depend in part on the number of replicates. If EV is detected within a pair (n = 2) at a concentration of a Test sample or the Standard, it will not always be clear which of the replicates is aberrant, and the laboratory should eliminate the concentration from further processing. If more than two replicates are performed at each dilution the laboratory may choose to adopt a strategy that identifies which of the extremes may be the outlier. Alternatively, the laboratory may choose to eliminate the dilution from further processing.
Model-Based Approaches—
Model-based approaches may be used to detect outliers within bioassay data. These approaches use the residuals from the fit of an appropriate model. In general, if using model-based methods to identify potential outliers, the models used may make fewer assumptions about the data than the models used to assess suitability and estimate potency. For example, a non-parametric regression (smoothing) model may be useful.
Lastly, an alternative to discarding outlying data is to use robust methods that are less sensitive to influence by outlying observations. Use of the median rather than the mean to describe the data’s center exemplifies a robust perspective. Also, regression using the method of least squares, which underlies many of the methods in this chapter, is not robust in the presence of outliers. The use of methods such as robust regression may be appropriate but is not covered in the USP bioassay chapters.
4.9 Fixed and Random Effects in Models of Bioassay Response
The choice of treating factors as fixed or random is important for the bioassay design, the development experiments, the statistical analysis of data, and the bioassay validation. Fixed effects are factors for which all levels, or all levels of interest, are discretely present, like sample, concentration, temperature and duration of thaw, and incubation time. Data for a response at some level, or combination of levels, of a fixed factor, can predict future responses. Fixed effects are expected to cause a consistent shift in responses. Analysts study fixed effects by controlling them in the design and examining changes in means across levels of the factor.
Random effects are factors of which the levels in a particular run of an assay are considered representative of levels that could be present. That is, there is no expectation that any specific value of the random factor will influence response. Rather, that value may vary subject to some expected distribution of values and thus may be a source of variability. For example, there is no desire to predict assay response for a specific day, but there is interest in predicting the variation in response associated with the factor “day”. Examples of random effects include reagent lot, operator, or day if there is no interest in specific reagent lots, operators, or day as sources of variability. Analysts may study random effects by measuring the variance components corresponding to each random effect. Variance components can be estimated well only if there are an appreciable number of levels of each random effect. If there are, for example, only two or three reagent lots or analysts present, the variation associated with these factors will be poorly estimated.
Making a correct choice regarding treating a factor as fixed or random is important to the design of the assay and to proper reporting of its precision. Treating all factors as fixed, for example, leads to an understatement of assay variability because it ignores all sources of variability other than replication. The goal is to identify specific sources of variability that can be controlled, to properly include those factors in the design, and then to include other factors as random.
If the factor may switch from random to fixed effect or vice versa, the factor should normally be modeled as a random effect. For example, reagent lots cannot be controlled, so different lots are typically considered to cause variability, and reagent lot would be considered a random effect. However, if a large shift in response values has been traced to a particular lot, a comparison among a set of lots could be performed using reagent lot as a fixed effect. Similarly, within-assay location (e.g., block, plate, plate row, plate column, or well) or sequence may be considered a source of random variation or a source of a consistent (fixed) effect.
Assay designs that consist of multiple factors are efficient, but require corresponding statistical techniques that incorporate the factors as fixed or random effects in the analysis. If all factors are fixed, the statistical model is termed a fixed-effects model. If all are random, it is termed a random-effects model. If some factors are fixed and some random, the model is a mixed-effects model. Note that the concepts of fixed and random effects apply to models for quantitative, qualitative and integer responses. For assay designs that include multiple experimental units (e.g., samples assigned to sets of tubes and concentrations assigned to pre-plate tubes) a mixed-effects model in which the experimental units are treated as random effects is particularly effective. Additional complexity is added by the presence of designs with crossed random effects (e.g., each operator used material from one or more reagent batches, but many reagent batches were used by multiple operators). This can cause methodological and computational challenges for model fitting, especially when the designs are unbalanced.
5. STAGES IN THE BIOASSAY DEVELOPMENT PROCESS
Given the ubiquity of cell-based assays and the motivation to use one bioassay system to provide context for discussion, the development of a cell-based bioassay will be used to illustrate the stages in the bioassay development continuum.
5.1 Design: Assay Layout, Blocking, and Randomization
Most cell-based assays are performed using a cell culture plate (6-, 12-, 96-, or 384-well micro titer plate). Ideally, a plate is able to provide a uniform substrate for experimental treatments in all wells, including after wash steps and incubations. However, regardless of assay conditions intended to minimize the potential for bias (e.g., good analyst technique, careful calibration of pipets, controlled incubation time, and temperature), systematic gradients on the plate, independent of experimental treatments, may be observed. These gradients may occur across rows, across columns, or from the edge to the center of the plate and are often called plate effects. Even moderate or inconsistent plate effects should be addressed during assay development, by means of plate layout strategies, blocking, randomization, and replication.
Plate effects can be evaluated in a uniformity trial in which a single experimental treatment, such as an assay concentration chosen from the middle section of the concentration–response curve, is used in all wells of the plate. Figure 1 provides an example of what may be observed; a trend of decreasing signal is evident from right to left. In this case, it was discovered that the plate washer was washing more briskly on the left side of the plate, and required adjustment to provide uniform washing intensity and eliminate the gradient. Another common plate effect is a differential cell-growth pattern in which the outer wells of the plate grow cells in such a way that the assay signal is attenuated. This is such a persistent problem that the choice is often made to not use the outer wells of the assay plate. Because location effects are so common, designs that place replicates (e.g., of sample by concentration combinations) in adjacent wells should be avoided.
Blocking is the grouping of related experimental units in experimental designs. Blocks may consist of individual 96-well plates, sections of 96-well plates, or 96-well plates grouped by analyst, day, or batch of cells. The goal is to isolate any systematic effects so that they do not obscure the effects of interest. A complete block design occurs when all levels of a treatment factor (in a bioassay, the primary treatment factors are sample and concentration) are applied to experimental units for that factor within a single block. An incomplete block design occurs when the number of levels of a treatment factor exceeds the number of experimental units for that factor within the block.
Randomization is a process of assignment of treatment to experimental units based on chance so that all such experimental units have an equal chance of receiving a given treatment. Although challenging in practice, randomization of experimental treatments has been advocated as the best approach to minimizing assay bias or, more accurately, to protecting the assay results from known and unknown sources of bias by converting bias into variance. While randomization of samples and concentrations to individual plate wells may not be practical, a plate layout can be designed to minimize plate effects by alternating sample positions across plates and the pattern of dilutions within and across plates. Where multiple plates are required in an assay, the plate layout design should, at a minimum, alternate sample positions across plates within an assay run to accommodate possible bias introduced by the analyst or equipment on a given day. It is prudent to use a balanced rotation of layouts on plates so that the collection of replicates (each of which uses a different layout) provides some protection against likely sources of bias.
Figure 2 illustrates a patterned assay design that lacks randomization and is susceptible to bias. Dilutions and replicates of the Test preparations (A and B) and the Standard (R) are placed together sequentially on the plate. Bias due to a plate or incubator effect can influence some or all of the concentrations of one of the samples. Note that in Figures 2 through 5 all outer plate wells are left as blanks to protect against edge effect.
A layout that provides some protection from plate effects and can be performed manually is a strip-plot design, shown in Figure 3. Here samples are randomized to rows of a plate and dilution series are performed in different directions in different sections (blocks) on the plate to mitigate bias across columns of the plate. An added advantage of the strip-plot design is the ability to detect location effects by the interaction of sample and dilution direction (left-to-right or right-to-left).
Figure 4 illustrates an alternation of Test (Test sample 1 = “1”; Test sample 2 = “2”) and Standard (“R”) positions on multiple plates, within a single assay run; this protects against plate row effects. Combining the two methods illustrated if Figures 3 and 4 can effectively help convert plate bias into assay variance. Assay variance may then be addressed, as necessary, by increased assay replication (increased number of plates in an assay).
A split-plot design, an alternative that assigns samples to plate rows randomly and randomizes dilutions (concentrations) within each row, is seen in Figure 5. Such a strategy may be difficult to implement even with the use of robotics.
Dilution Strategy—
Assay concentrations of a Test sample and the Standard can be obtained in different ways. Laboratories often perform serial dilutions, in which each dilution is prepared from the previous one, in succession. Alternatively, the laboratory may prepare wholly independent dilutions from the Test sample and Standard to obtain independent concentration series. These two strategies result in the same nominal concentrations, but they have different properties related to error. Serial dilutions are subject to propagation of error across the dilution series, and a dilution error made at an early dilution will result in correlated, non-independent observations. Correlations may also be introduced by use of multichannel pipets. Independent dilutions help mitigate the bias resulting from dilution errors.
It is noteworthy that when working to improve precision, the biggest reductions in variance come when replicating at the highest possible levels of nested random effects. This is particularly effective when these highest levels are sources of variability. To illustrate: replicating extensively within a day for an assay known to have great day-to-day variation is not effective in improving precision of reportable values.
5.2 Development
A goal of bioassay development is to achieve optimal bioassay relative accuracy and precision of the potency estimate. An endpoint of assay development is the completed development of the assay procedure, a protocol for the performance of the bioassay. The procedure should include enough detail so that a qualified laboratory with a trained analyst can perform the procedure in a routine manner. A strategic part of development is a look forward toward performance maintenance. Standard operating procedures for reagent and technician qualification, as well as for calibration of the working Standard, help complete the bioassay development package.
One Factor at a Time versus Design of Experiments—
Bioassay development proceeds through a series of experiments in which conditions and levels of assay factors are varied to identify those that support a reliable and robust bioassay qualified for routine use. Those experiments may be conducted one factor at a time (OFAT), studying each parameter separately to identify ideal conditions, or through the use of multi-factor design of experiments (DOE). DOE is an efficient and effective strategy for developing a bioassay and improving bioassay performance, thus helping to obtain a measurement system that meets its requirements. In comparison to OFAT, DOE generally requires fewer experiments and also provides insight into interactions of factors that affect bioassay performance. Assay development using DOE may proceed through a series of steps: process mapping and risk analysis; screening; response optimization; and confirmation.
Process Mapping and Risk Analysis—
Bioassay optimization may begin with a systematic examination and risk assessment to identify those factors that may influence bioassay response. It is useful to visualize bioassay factors using a bioassay process map such as a cause-and-effect or fishbone diagram. Using the process map as a guide, the laboratory can examine assay factors that might affect assay performance, such as buffer pH, incubation temperature, and incubation time. Historical experience with one or several of the bioassay steps, along with sound scientific judgment, can identify key factors that require further evaluation. One tool that may be used to prioritize factors is a failure mode and effects analysis. Factors are typically scored by the combination of their potential to influence assay response and the likelihood that they will occur. The laboratory must be careful to recognize potential interactions between assay factors.
Screening—
Once potential key factors have been identified from process mapping and risk analysis, the laboratory may conduct an initial screening experiment to probe for effects that may require control. Screening designs such as factorial and fractional factorial designs are commonly used for this purpose. Software is available to assist the practitioner in the selection of the design and in subsequent analysis. Analysts should take care, however, to understand their assumptions about design selection and analysis to ensure accurate identification of experimental factors.
Response Optimization—
A screening design will usually detect a few important factors from among those studied. Such factors can be further studied in a response-optimization design. Response-optimization designs such as central composite designs are performed to determine optimal settings for combinations of bioassay factors for achieving desired response. The information obtained from response optimization may be depicted as a response surface and can be used to establish ranges that yield acceptable assay performance and will be incorporated into the bioassay procedure.
In the parlance of Quality by Design (QbD), the “region” where the combined levels of input variables and process parameters have been demonstrated to provide acceptable assay performance is described as the design space for the bioassay. Establishing a true design space for a bioassay is challenging; some but not all factors and levels of random factors will be included in the development DOE, and there is no assurance that the design space is not sensitive to unstudied random factors. Similarly, there is little assurance that the assay (design space) is robust to random factors that are studied using small samples (or non-random samples of levels). Elements of DOE that may be considered include the use of blocks; deliberate confounding among interactions that are of lower interest, or known to be unimportant; robust design (response surface designs with random effects); and use of split-plot, strip-plot, or split-lot designs.
Confirmation—
The mathematical model depicting assay performance as a function of changes in key assay factors is an approximation; thus, it is customary to confirm performance at the ideal settings of the bioassay. Confirmation can take the form of a qualification trial in which the assay is performed, preferably multiple independent times using optimal values for factors. Alternatively, the laboratory may determine that the bioassay has been adequately developed and may move to validation. Qualification is a good practice, not a regulatory requirement. The decision to perform confirmatory qualifying runs or to proceed to validation depends upon the strength of the accumulated information obtained throughout development.
5.3 Data Analysis during Assay Development
Analysis of bioassay data during assay development enables analysts to make decisions regarding the statistical model that will be used for routine analysis, including transformation and/or weighting of data, and the development of system and sample suitability criteria. The analysis also provides information regarding which elements of design structure should be used during outlier detection and the fitting of a full model. This may also include a plan for choosing subsets of data, such as a linear portion, for analysis or, for nonlinear bioassays, a model reduction strategy for samples similar to Standard. Once these decisions are made and proven sound during validation, they don’t need to be reassessed with each performance of the assay. A process approach to enabling these decisions follows.
Step 1: Choose an appropriate statistical model (also see section 4.6 Common Bioassay Models).
Given the complexity of bioassays and the motivation to use an approach proven reliable, fairly standardized analytical models are common in the field of bioassay analysis. Nonetheless, many considerations are involved in choosing the most appropriate statistical model. First, the model should be appropriate for the type of assay endpoint—continuous, count, or dichotomous. Second, the model should incorporate the structure of the assay design. For any design other than completely randomized, there will be terms in the model for the structural elements. These could be, for example, within-plate blocking, location of cage in the animal facility, day, etc. A third consideration, applicable to continuous endpoints, involves whether to use a regression model or a means model (an analysis of variance model that fits a separate mean at each dilution level of each sample tested), with appropriate error terms. A means model can be appropriate at this stage because it makes no assumptions about the shape of the concentration–response curve.
Step 2: Fit the chosen statistical model to the data without the assumption of parallelism, and then assess the distribution of the residuals, specifically examining them for departures from normality and constant variance.
Transform the data as necessary or, if needed, choose a weighting scheme (see section 4.3 Variance Heterogeneity, Weighting, and Transformation). Use as large a body of assay data, from independent assays, as possible. The primary goal is to address any departure from normality and from constant variance of responses across the range of concentrations in the assay. Step 2 will likely alternate between imposing a transformation and assessing the distribution of the residuals.
Step 3: Screen for outliers, and remove as is appropriate.
This step normally follows the initial choice of a suitable transformation and/or weighting method. Ideally the model used for outlier detection contains the important elements of the assay design structure, allows nonsimilar curves, and makes fewer assumptions about the functional shape of the concentration–response curve than did the model used to assess similarity. See section 4.8 Outliers and general chapter  1010
1010 for discussion of outlier detection and removal. In some cases, outliers may be so severe that a reasonable model cannot be fit, and thus residuals will not be available. In such cases, it is necessary to screen the raw data for outliers before attempting to fit the model.
for discussion of outlier detection and removal. In some cases, outliers may be so severe that a reasonable model cannot be fit, and thus residuals will not be available. In such cases, it is necessary to screen the raw data for outliers before attempting to fit the model.
During assay development, a strategy should be developed for the investigation and treatment of an outlier observation, including any limits on how many outliers are acceptable. Include these instructions in the assay SOP. Good practice includes recording the process of an investigation, outlier test(s) applied, and results therefrom. Note that outlier procedures must be considered apart from the investigation and treatment of an out-of-specification (OOS) result (reportable value). Decisions to remove an outlier from data analysis should not be made on the basis of how the reportable value will be affected (e.g., a potential OOS result). Removing data as outliers should be rare. If many values from a run are removed as outliers, that run should be considered suspect.
Step 4: Refit the model with the transformation and/or weighting previously imposed (Step 2) without the observations identified as outliers (Step 3) and re-assess the appropriateness of the model.
Step 5: If necessary or desired, choose a scheme for identifying subsets of data to use for potency estimation, whether the model is linear or nonlinear (see section 4.5 Linearity of Concentration–Response Data).
Step 6: Calculate a relative potency estimate by analyzing the Test and Standard data together using a model constrained to have parallel lines or curves, or equal intercepts.
5.4 Bioassay Validation
The bioassay validation is a protocol-driven study that demonstrates that the procedure is fit for use. A stage-wise approach to validation may be considered, as in a “suitable for intended use” validation to support release of clinical trial material, and a final, comprehensive validation prior to BLA or MAA filing. Preliminary system and sample suitability controls should be established and clearly described in the assay procedure; these may be finalized based on additional experience gained in the validation exercise. Chapter  1033
1033 provides validation comprehensive discussion of bioassay validation.
provides validation comprehensive discussion of bioassay validation.
5.5 Bioassay Maintenance
The development and validation of a bioassay, though discrete operations, lead to ongoing activities. Assay improvements may be implemented as technologies change, as the laboratory becomes more skilled with the procedure, and as changes to bioassay methodology require re-evaluation of bioassay performance. Some of these changes may be responses to unexpected performance during routine processing. Corrective action should be monitored using routine control procedures. Substantial changes may require a study verifying that the bioassay remains fit for use. An equivalence testing approach can be used to show that the change has resulted in acceptable performance. A statistically-oriented study can be performed to demonstrate that the change does not compromise the previously acceptable performance characteristics of the assay.
Assay Transfer—
Assay transfer assumes both a known intended use of the bioassay in the recipient lab and the associated required capability for the assay system. These implicitly, though perhaps not precisely, demarcate the limits on the amount of bias and loss of precision allowed between labs. Using two laboratories interchangeably to support one product will require considering the variation between labs in addition to intermediate precision for sample size requirements to determine process capability. For a discussion and example pertaining to the interrelationship of bias, process capability, and validation, see A Bioassay Validation Example in  1033
1033 .
.
Improving or Updating a Bioassay System—
A new version of a bioassay may improve the quality of bias, precision, range, robustness, specificity, lower the operating costs or offer other compelling advantages. When improving or updating a bioassay system a bridging study may be used to compare the performance of the new to the established assay. A wide variety of samples (e.g., lot release, stability, stressed, critical isoforms) can be used for demonstrating equivalence of estimated potencies. Even though the assay systems may be quite different (e.g., an animal bioassay versus a cell-based bioassay), if the assays use the same Standard and mechanism of action, comparable potencies may reasonably be expected. If the new assay uses a different Standard, the minimum requirement for an acceptable comparison is a unit slope of the log linear relationship between the estimated potencies. An important implication of this recommendation is that poor precision or biased assays used early can have lasting impact on the replication requirements, even if the assay is later replaced by an improved assay.
Auxiliary Information—
Please check for your question in the FAQs before contacting USP.
| Topic/Question | Contact | Expert Committee |
|---|---|---|
| General Chapter | Tina S. Morris, Ph.D.
Vice President, Biologics & Biotechnology (301) 816-8397 |
(STAT2010) Statistics 2010 |
USP38–NF33 Page 769
Pharmacopeial Forum: Volume No. 36(4) Page 956