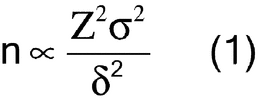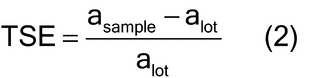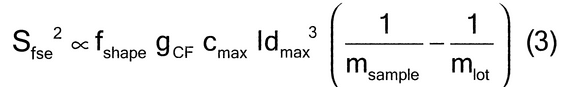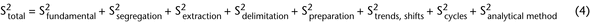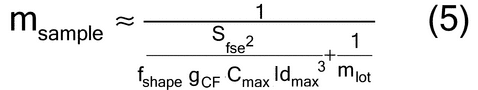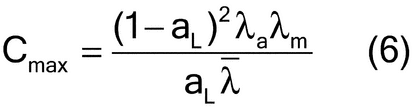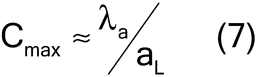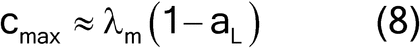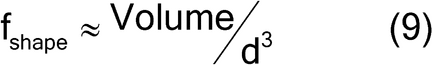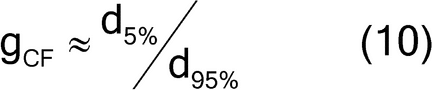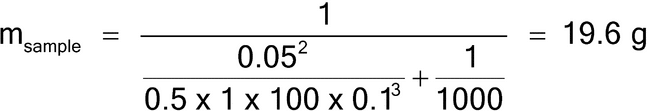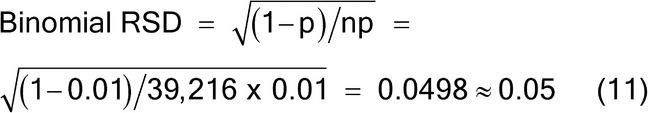INTRODUCTION
The goals of this chapter are to provide guidance on bulk powder sampling procedures, identify important bulk powder sampling concepts, and collect a knowledge base of useful practices and considerations that can lead to the ideal physical sampling of bulk powder materials. The terminology used here is well established in the field of material sampling (see Appendix 3, for instance reference 7). Sampling is undertaken as part of an estimation process. The parameter of primary interest here is the mean level of some analyte in the bulk powder as a whole.
The purpose of a sampling plan is to obtain a representative sample of a population so that reliable inferences about the population sampled can be drawn to a certain level or degree of confidence. Acquiring a representative sample from a lot is critical because without a representative sample all further analyses and data interpretations about the lot are in doubt. An ideal sampling process is a process in which every particle or at least every equal-size portion of the population has an equal probability of being chosen in the sample. In addition, sampling procedures should be reproducible, i.e., if the sampling protocol were repeated, a high probability should exist of obtaining similar results. Also, the integrity of the sample should be preserved during and after sampling. The details of how to sample depend on a variety of factors. For example, criteria for sampling to evaluate particle segregation may differ from criteria for evaluating moisture content or identification.
Because of the propensity of a powder to segregate, heterogeneous powder systems can make it difficult to obtain an ideal sample. Thus, to extract representative samples requires careful development of a sampling plan that accounts for and mitigates the segregation tendencies of a particular powder system. Developing a general guidance for bulk powder sampling is challenging because every situation is different, and therefore different approaches must be used to deal with each situation. Thus, the goal of this general information chapter is to outline recommended steps for developing a sampling scheme or plan for a particular system that is consistent with good sampling practices.
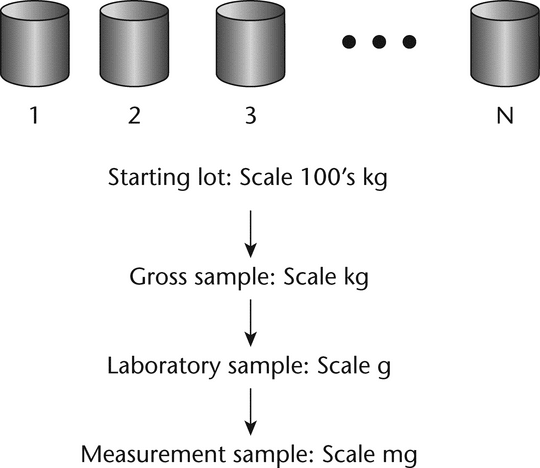
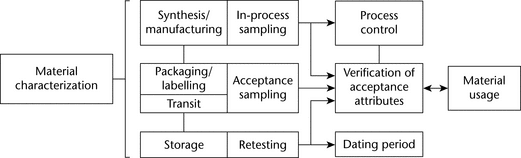
The primary difficulty in acquiring a representative sample is that the size of the sample for measurement, typically a few milligrams to grams, must be withdrawn from a large population on the order of hundreds to thousands of kilograms. The few milligrams analyzed in a laboratory must be taken from a large population of particles in a warehouse in such a manner that the measurement sample is representative of all the particles in the lot. Any bias or error in the sampling process will cause all future inferences to be in error. Over the years methods have been developed and refined to attempt to ensure that the measurement sample is representative of the whole population. A typical strategy is shown in Figure 1. The strategy is to sample in stages, starting with the initial gross or primary sample withdrawn directly from the received containers. In the laboratory, the gross sample must be reduced in size until it is the appropriate size for measurement. This should be done in a manner that minimizes the introduction of sampling errors. The key to reducing the sampling error is to ensure that every particle of the population has an equal probability of being included in the sample. However, because of segregation or the nonrandom nature of powders, many obstacles can cause bias and contribute to sampling errors. Following the flow chart in Figure 1 and the steps outlined in subsequent discussions will help to minimize sampling errors.
Figure 1. Overall sampling strategy for reducing the sample size from the hundreds of kg scale to the mg scale.
To acquire a representative sample, a suitable sampling plan must be developed and implemented. A good sampling plan includes: (1) population determination and sample size selection, (2) a sample collection procedure and a method for sample size reduction, and (3) summary calculations that demonstrate that the sampling plan will yield samples that accurately characterize the population to within a stated level of acceptance. In addition, an infrastructure is needed to maintain the integrity of the samples and sampled materials.
This chapter begins with a brief introduction to sampling theory and terminology. The technical content of the chapter requires a basic scientific understanding of physical particle characteristics (e.g., mass, density, shape, and size) and statistics (e.g., acceptance sampling and binomial distribution).
SAMPLING THEORY AND TERMINOLOGY
Fundamental Sample Size (Sample Mass)
Sample size is considered from two perspectives: (1) the mass of the sample intended to represent the entire population, sometimes termed the composite sample, and (2) the number of samples taken with a mass sufficient to independently evaluate, compare, or provide confidence to ensure the reproducibility of the composite or the uniformity of the population. The key to obtaining an ideal sample is to understand and account for the degree of heterogeneity of the characteristic being evaluated in the system under study. For example, heterogeneity of a particle system arises from two sources: the intrinsic, constitutive, or compositional heterogeneity and the spatial distribution heterogeneity. The intrinsic heterogeneity of the powder system reflects the fundamental differences in the individual particles. Statistical heterogeneity (differences between individuals), or variance, is expected to maintain assumed properties. For a normal population the general expression for a statistical sample size suggests that the number of independent samples is proportional to the square of the normal quantile at the desired confidence level (Z) and the population variance ( 2) and is inversely proportional to the square of the mininum detectable difference required (
2) and is inversely proportional to the square of the mininum detectable difference required ( ), as shown in equation 1:
), as shown in equation 1:
In order to apply the normal theory sample size equation to sample mass with a discrete number of particles, consideration for material characteristics is needed. For a heterogeneous bulk material, such as a bulk powder, the sample mass required to ensure adequate representation of the intrinsic or fundamental population heterogeneity or variation is determined by the size, shape, and density of the particles. The total sampling error (TSE) measures the difference between the analyte concentration estimated in the sample (asample) and the mean analyte concentration in the lot (alot) relative to the mean analyte concentration in the lot (alot), as shown in equation 2:
When ideal sampling is employed, the TSE is reduced to a fundamental sampling error, limited only by the intrinsic heterogeneity of the material. The relative variance of the fundamental sampling error (Sfse2) has been empirically estimated in particle size applications by characterizing the critical particle mass, heterogeneity, size (diameter), shape, density, and weights of the material. Empirical estimates require a thorough and complete knowledge of the material and process. Established material characterization and methods are critical aspects of avoiding unacceptable estimates. As shown in equation 3:
where fshape is a measure of cubicity or shape factor of the analyte particles; gCF, the granulometric factor, is an empirical correction factor of differences in particle size; cmax is the compositional maximum heterogeneity and is calculated as if the material consists of the analyte particles and everything else; l, the liberation factor, is an empirical factor representing the proportion of critical content particles separated from the non-analyte containing particles of the lot; dmax is the particle diameter [e.g., the maximum diameter or the diameter (cm) of the size of the opening of a screen retaining 5% by weight of the lot to be sampled]; msample is the mass of the sample; and mlot is the mass of the lot being sampled. [Note—A liberation factor is needed when the analyte does not appear as separate particles. A high liberation value (1.0) suggests heterogeneity of particles. A low liberation value (0.05) suggests very homogeneous particles. See Appendix 1 for examples of potential applications of equation 3 in the estimation of the fundamental sample mass needed to account for constitutional heterogeneity of the powder mixture. ] Use of equation 3 requires prior estimates of fshape, gCF, cmax, I, and dmax.
Segregation Error
Distribution heterogeneity is the difference between samples or groups of particles spatially or temporally. For example, small particles are located preferentially in the lower portion of a powder bed. This type of situation can arise as a result of powder bed segregation and is common in some particle systems with a broad particle size distribution. In other words, smaller particles may not be randomly distributed throughout the lot. This spatial heterogeneity introduces variation in the sample and is a source of variation that contributes to the total variation. Together, fundamental and segregation error give rise to sampling error, which dictates how variable the samples will be, how large the sample size and numbers of samples should be (e.g., 10 containers, sampled at top and bottom, with sample sizes of 50 g each), and how hard it will be to obtain a representative sample.
Minimizing the effects of segregation error during lot material characterization while still ensuring a representative sample mass requires collecting many small samples that average out the variation of the segregation error. This assumes one is interested in estimating the overall average, not characterizing lot heterogeneity. Segregation error is difficult to control because segregation may be the result of changes in particle size, shape, and density, as well as inputs into the determination of sample mass. Minimizing the effects of segregation error when reducing the primary sample size requires adequate physical mixing or randomization of the primary samples before analysis, thus providing equal selection probability.
Total Sampling Method Error
Intrinsic or compositional heterogeneity is a function of the powder system and represents the true characteristics of the material (e.g., equation 3). Thus, intrinsic heterogeneity is often the minimal variance a system can have. The difference between the true state of the system and what is actually measured when ideal sampling is employed is called the fundamental error (equation 2). The relative variance of TSE (S2Total) is represented in equation 4 as the sum of the relative variances of all error components:
The S2Total can be reduced by employing ideal sampling. Ideal sampling will limit or adjust for the effects of error contributed by particle segregation, extraction error created by the sampling device, delimitation error created by not considering the three-dimensional nature of the bulk material, and sample handling errors such as product degradation. The total variation is the sum of these sources of error, illustrated in equation 4 as independent, additive components. To the end of reducing these errors, an important goal of material characterization by sampling is the determination of the relevant errors within the bulk sample. Knowing the source of the error helps determine how to best minimize these errors.
Fundamental error arises from the intrinsic heterogeneity of particles within a sample of the material population. Reducing fundamental error requires changing the intrinsic characteristics of the material, such as reducing the particle size by milling or grinding. Segregation error is the spatial distributional difference of particles across the population. This type of error can be minimized by mixing or randomization of the particles being selected. Segregation error is affected by the characteristics of fundamental error. Additionally, for the determination of both fundamental and segregation error, it is assumed that mechanical sampling is carried out correctly and is not invasive, i.e., that mechanical sampling does not alter the characteristics being measured and provides a true representation. In instances where sampling of the bulk material does not provide unbiased representation or is so invasive that it alters material characteristics, then, in order to obtain noninvasive, unbiased samples, operators may need to change sampling from a bulk form to a stream form of processing, either upstream or downstream from the sample point (see Appendix 2). The mechanical sampler may need to mix the sample sufficiently to facilitate random sampling with equal probability of selection in order to obtain an adequate representation of the entire bulk lot. The process may also require mixing or sampling from a location in the process that will provide a random sample from material that is susceptible to segregation.
Extraction, delimitation, and handling errors occur as a result of the mechanical sampler and sample handling prior to analysis, which also are affected by fundamental error. Trends, shifts, and cycles are temporal sources of error that affect total error. The analytical error of the method of analysis contributes to the overall error of the reported result. In addition to obtaining representative subsamples from the bulk material, the method must also obtain a representative subsample from the particulate laboratory sample before analysis.
Sampling Strategy
A typical sampling strategy consists of two basic steps: (1) the primary or gross sample, followed by (2) the secondary sample, which reduces the primary sample to a size that is suitable for laboratory measurement. In short, the goal is to select from the lot a quantity of material suitable for measurement without significantly changing the attribute for which one is sampling. In parallel with the sample size reduction, sample size calculations must be done in such a way that the sampling strategy has sufficient statistical power to determine whether the attributes of interest lie within the specification ranges with a reasonable degree of certainty. Each step must be done correctly, or the sampling strategy as a whole will not provide a sample that is representative of the original population.
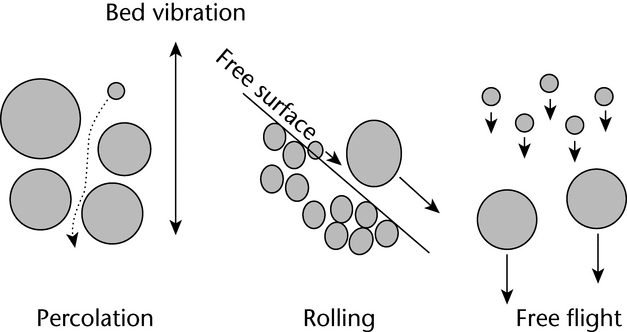
To successfully withdraw a sample from a bulk container that is representative of the population, one needs to have an idea of the population's heterogeneity, i.e., how segregated or stratified the system is. Knowing what factors can accentuate segregation and knowing the patterns of segregation that are likely will help one to account for segregation in a powder bed and to take better samples. Many factors can affect the degree of powder bed segregation. For segregation to occur, sufficient energy needs to be put into the powder bed to induce motion between particles. When a sufficient amount of energy is supplied, segregation can occur via three modes: percolation (in the powder bed), rolling (on the free surfaces of a powder bed), and free flight (when the powder bed is fluidized). These modes are illustrated in Figure 2.
Figure 2. Illustration of the three modes of particle segregation: percolation, rolling, and free flight.
Within the powder bed, segregation can occur by means of percolation, also called sifting segregation, as well as through the movement of coarse particles to the top via vibration. During sifting segregation, smaller particles acting under the influence of gravity can more easily migrate downward into the void spaces between larger particles when the particle bed is perturbed. The net effect of these movements is that the smaller particles percolate down into the powder bed, resulting in the top of the powder bed having a higher proportion of larger particles. A common example of sifting segregation is unpopped corn kernels that are found at the bottom of a bag of popped popcorn.
For free surfaces, rolling segregation can occur any time that particles can roll down a free surface. In other words, segregation can occur on any non-level surface that allows the relative movement of particles. When particles roll down these free surfaces, larger particles tend to tumble farther down the surface than the smaller particles (see Figure 3). For example, if a conical heap or pile is formed in the middle of a hopper during loading, larger particles are more likely to roll farther down the heap, toward the outer edge of the hopper. This creates a situation in which the smaller particles tend to be in the center of the hopper, and the larger particles accumulate toward the outer wall of the hopper. The formation of these free surfaces can be a major factor in segregation.
When powder beds are fluidized, a large amount of air is incorporated into the powder bed and, when this air is moving, the air velocity may exceed the terminal velocity of the smaller particles. When this happens, the fine particles are suspended in the air stream while the coarse particles settle out. The fine particles eventually settle on top of the powder bed, forming a top layer that has a higher concentration of fine particles. This type of segregation, sometimes called elutriation segregation, can occur when a powder is discharged from a hopper, or is poured into the top of a hopper, and a large volume of air is displaced.
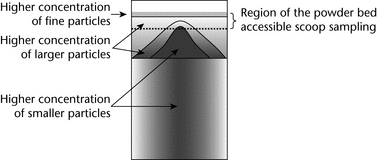
In summary, for a highly segregating system, the powder bed could have a particle distribution similar to that shown in Figure 3, where, as a result of elutriation segregation, a layer of fine particles on the top overlies larger particles deposited by percolation segregation, and a radial distribution of larger particles appears toward the outer wall as a result of rolling segregation.
In general, the primary factors that affect segregation are particle size and size distribution, density, and shape and shape distribution. Of secondary importance are surface roughness, surface coefficient of friction, moisture content, and container shape and design. Particle size is the most important single factor, and subtle differences in particle size can cause measurable segregation. If the attribute of interest is associated with particle size, then this attribute will segregate along with the different particle sizes. For example, if a manufacturer makes a granulation in which the larger particles contain more drug than the smaller particles, then drug content can be very prone to segregation—i.e., drug content will show segregation patterns similar to those associated with particle size segregation.
Segregation can notably increase sampling error because it decreases the probability that certain particle types will be in the sample. In addition, the powder bed may already be segregated when material is received, and poor sample handling can also cause segregation. To avoid further segregation during sample handling, the operator should avoid situations that promote segregation, such as the following: pouring where the powder forms a sloping surface, pouring into the core of a hopper, vibrations, shaking, and stirring (unless done to promote mixing). In addition, the use of mass flow hoppers reduces segregation.
Two basic strategies help promote ideal sampling: (1) use of a sampling thief and (2) sampling from a moving powder stream.
A sampling thief is a long spearlike probe that can be inserted into the powder bed and, once inserted, can collect powder samples from points adjacent to the spear. With a sampling thief, particles from almost any point in the powder bed can be included in the sample. The second method relies on fundamental principles of sampling, namely that (1) a powder should always be sampled when in motion, and (2) the whole stream of powder should be sampled for many short periods rather than sampling a part of the stream for a longer period.
For example, if the container to be sampled is emptied onto a conveyer belt, all the material will pass by a single point that can be sampled. Thus, no matter how segregated the system is, the collection of the powder at random time points ensures that every particle has an equal probability of being included in the sample. The second fundamental principle accounts for material segregation on the conveyer belt: by collecting the entire stream, one gets a cross section of all the particles, no matter how much segregation occurs on the conveyer belt.
Many methods are available for obtaining a sample from a powder system. Unfortunately, many of these methods involve setting the powder bed in motion or performing in-process sampling. Because of concerns about cross-contamination and containment of potentially toxic materials, most of these methods are impractical for the bulk sampling required for compliance with current Good Manufacturing Practices (cGMPs). Hence, most of the sampling done in the pharmaceutical industry is static sampling, done by either (1) scoop or grab sampling or (2) stratified sampling, typically employing a sampling thief. The choice of method is dictated by the distribution of the attribute being sampled in the container, as discussed below.
GENERAL SAMPLE COLLECTION: CONSIDERATIONS AND TOOLS
Types of Systems and General Considerations
Homogeneous Systems:
For powder systems where the attribute of interest is uniformly distributed throughout the container—so that any sample is an unbiased representation of the entire container, lot, or population of interest—scoop sampling is adequate. Scoop sampling is a straightforward procedure in which the operator, after selecting representative containers for sampling, opens a container, scoops out a sufficient amount of material from the top of the powder bed, and then seals the container. If a thin layer of material on top of the powder bed is suspected of being different from the bulk, samples should be taken from a point below this top layer. For example, in cases of elutriation segregation, a thin layer of fine particles may lie on top of the powder bed, and the operator should dig down into the powder bed to avoid sampling from this layer. The scoop should be large enough that no material is lost during handling, because lost material may result in sample bias. In other words, one should avoid the use of a heaping scoop from which material can roll off the sides. The advantages of scoop sampling are convenience and cost, and, for highly potent materials, low-cost disposable scoops that can be used to minimize cross-contamination.
Heterogeneous Systems:
If the attribute of interest is spatially distributed in a heterogeneous manner throughout the sample, then scoop sampling is prone to potentially significant errors. Scoop sampling is a non-probabilistic method because only the most accessible fraction of the container is sampled. Obviously, only the material in the top layer can be reached with a scoop. For example, a sample from the top outer edge of the drum shown in Figure 3 could be biased because, in this example, the larger particles are preferentially distributed toward the top and outer edges of the drum. Hence the smaller particles have a lower probability of appearing in the sample. As a result, the smaller particles will be underrepresented in the sample, and any analysis of particle size will not reflect the true particle size distribution of the original population.
For heterogeneous systems, the initial primary sample is the most difficult to obtain. Use of a sampling thief, sometimes called a grain probe or sampling spear, is needed. The advantage of a sampling thief is that much more of the powder bed is accessible because the sampling thief can sample from different points in the powder bed, thus helping to reduce sampling bias. Many types of sampling thieves are available, including: (1) the concentric sleeve with slotted compartments, (2) the concentric sleeve with grooves, sometimes called the open-handled probe, (3) the end sampler, and (4) the core sampler. Each type has its own unique operating procedures, as described below.
The concentric sleeve with slotted compartments is probably the most popular type of sampling thief used in the pharmaceutical industry. This type consists of two concentric tubes or cylinders in which the inner tube is divided into compartments. This design makes it possible to detect differences in the attribute of interest across the depth of the container. To collect a sample, the operator closes the compartments and inserts the sampling thief into the powder bed with the collection zone openings facing upward. The handle is turned to open the sample zones, then the handle is moved up and down with two quick short strokes to help fill the compartments. The sampling thief is then closed and removed from the powder bed. The operator should visually inspect the powder bed through its depth before emptying the sampling thief. The powder from the individual compartments can be combined on a clean surface or in a collection container. In certain situations the material from each compartment may be analyzed separately, that is, without mixing.
In the concentric sleeve with grooves (open-handled probe), the inner tube is not divided into compartments. The probe is first inserted into the powder bed with the groove open, the outer sleeve is rotated to close, and the sampling thief is then withdrawn from the powder bed. The probe’s contents are emptied from the handle end by holding the probe upright and letting the sample slide out from the handle, a method more convenient than the one using the thief with slotted compartments. However, this type of thief makes it more difficult to perform visual inspection to examine for material inconsistencies according to depth.
An end sampler probe, often used to sample slurries, has a single entry zone at the bottom of the sampling thief. Frequently the end sampling zone is larger than the rest of the sampling thief. This feature is a disadvantage because the larger the probe, the more it perturbs the powder bed, possibly resulting in the introduction of sampling bias.
Core samplers have a hollow outer cylinder with a tapered outer wall on the open end. This probe is inserted into the powder bed, and the intrinsic cohesion of the particles keeps them from flowing out when the probe is withdrawn. The contents of the cylinder are then emptied into a clear container.
General Considerations:
The most reliable and reproducible results in powder size measurements are obtained when the particle size ranges from 2 to 10 µm; otherwise, the powder is too cohesive and does not flow properly into the sampling thief. In addition, particles larger than about one-third the width of the slot give poor results. Samples should be taken from several sites throughout the container. The probe should be long enough to penetrate at least three-quarters of the depth of the powder bed, ensuring that material from all depths can be captured in the sample. The choice of sites should be dictated by an understanding (often subjective) of the powder bed's degree of heterogeneity, which may have been caused by handling or movement during transport. Sampling plans can call for the insertion of the probe either at random locations and random angles or at predetermined locations and angles. For example, the plan may call for the probe to be inserted at the center and at two locations near the edges. Also, many operators recommend that probes always be inserted at a 10 angle from vertical, which increases the range of locations sampled.
angle from vertical, which increases the range of locations sampled.
Some of the disadvantages of sampling thieves include the labor-intensive nature of the procedure. The probe must be physically inserted into the powder bed, often multiple times; the contents of the probe must be emptied; and then the probe must be thoroughly cleaned. For settled powder beds, the sampling probe can be difficult to insert. In addition, the sampling probe can introduce errors as a result of the following: fine particles can lodge between the inner and outer tubes; particles can fracture; fine particles can compact and not flow well into the sampling compartments; segregation can occur during flow into the sampling zone; and the act of inserting the probe can disrupt the powder bed by dragging powder from the top layers of the bed down through the bed.
Representative Lot Sampling
Statistically-based sampling plans are based on statistical principles and depend on the population’s spatial heterogeneity and intrinsic variability. Statistically-based plans are efficient and allow the collection of a sufficient number of samples to yield the desired degree of certainty without collecting too many or too few samples for the test method, scale, product variation, risk requirements, and tolerance for a stated product’s quality level or specification. The commonly used 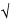 N + 1 sampling plan given in Table 1 is not a statistically based sampling plan and may result in collection of too few samples for small populations and too many samples for large populations. The use of statistically-based sampling plans is advantageous because it facilitates risk management. However, in cases where prior knowledge of the population to be sampled is insufficient, a nonstatistical sampling plan such as that given in Table 1 can be considered.
N + 1 sampling plan given in Table 1 is not a statistically based sampling plan and may result in collection of too few samples for small populations and too many samples for large populations. The use of statistically-based sampling plans is advantageous because it facilitates risk management. However, in cases where prior knowledge of the population to be sampled is insufficient, a nonstatistical sampling plan such as that given in Table 1 can be considered.
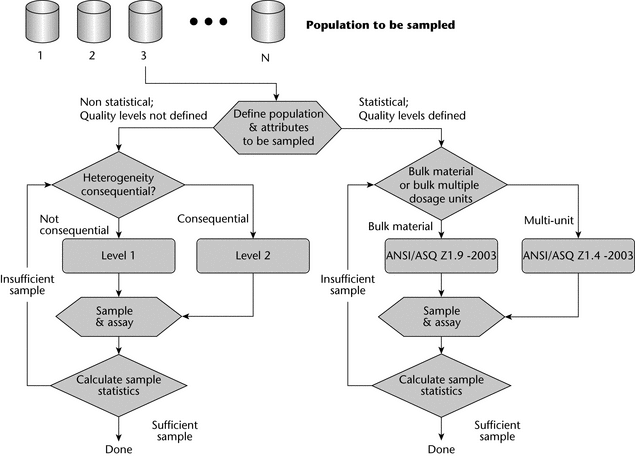
Figure 4 illustrates the sample size selection scheme paths. The first choice is whether to use a statistical or nonstatistical sampling plan. Statistical plans are preferred when a variable attribute like particle size or drug content is being determined. General sampling approaches are outlined in USP general information chapter Analytical Data—Interpretation and Treatment  1010
1010 . Statistically-based lot acceptance sampling plans require a valid rationale with known quality levels for the determination of product lot characteristics. As noted, the application of statistical sampling plans, including lot acceptance sampling plans, requires specific and thorough knowledge of the material being sampled. Reference statistical sampling plans state the rationale for sampling as part of the sampling scheme. Manufacturers who use a statistically-based lot acceptance sampling method should refer to an appropriate standard such as ANSI/ASQ Z1.9-2003 for bulk materials or ANSI/ASQ Z1.4-2003 for multiunit or discrete populations. These standards are readily available via sources such as the American Society for Quality (http://www.asq.org/) or the American National Standards Institute (http://www.ansi.org/).
. Statistically-based lot acceptance sampling plans require a valid rationale with known quality levels for the determination of product lot characteristics. As noted, the application of statistical sampling plans, including lot acceptance sampling plans, requires specific and thorough knowledge of the material being sampled. Reference statistical sampling plans state the rationale for sampling as part of the sampling scheme. Manufacturers who use a statistically-based lot acceptance sampling method should refer to an appropriate standard such as ANSI/ASQ Z1.9-2003 for bulk materials or ANSI/ASQ Z1.4-2003 for multiunit or discrete populations. These standards are readily available via sources such as the American Society for Quality (http://www.asq.org/) or the American National Standards Institute (http://www.ansi.org/).
If one is developing a nonstatistical sampling plan for which the quality level is not known, Table 1 gives suggested sample sizes for the number of containers in the lot that should be sampled.
The Level 1 sampling plan is relevant to materials when heterogeneity does not affect the analysis and the customer seeks to sample more than one container, when the sampling plan can be proportional to the square root of the number of containers received, and when the material comes from a known and trusted source. In such cases, the sample can be withdrawn from any point in the container. For adequately homogenous systems, scoop sampling from the top of the container is suitable.
The Level 2 sampling plan involves a 50% increase in sample size when compared with Level 1 and is used when a larger proportion of the number of containers is needed, for example, when a material’s heterogeneity is suspected of being consequential and acceptance sampling quality levels are not defined, or when the material comes from a less trusted source. Depending on the material's degree of heterogeneity, a sampling thief may be used. However, if the degree of heterogeneity will not significantly affect the results for the attribute being sampled, then scoop sampling from the top of the drum may still be suitable.
Table 1 shows the number of containers, n, to be sampled for a lot segregated into N containers. Note that the value of n from the formula is rounded at 0.5 up to the next higher integer. For example, if N = 6: for Level 1, n = 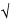 6 + 1 = 3.45 rounds to n = 3; for Level 2, n = 1.5 ×
6 + 1 = 3.45 rounds to n = 3; for Level 2, n = 1.5 × 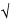 6 = 3.67, which rounds to n = 4.
6 = 3.67, which rounds to n = 4.
Table 1
| N (Number of Containers Comprising Lot) | n (Sample Size) | |
|---|---|---|
| Level 1 | Level 2 | |
| N |
AII | AII |
| N |
1.5 × |
|
These initial decisions, as illustrated in Figure 4, are often difficult and sometimes must be made without sufficient information. If there is uncertainty about which method or level is appropriate, sometimes a quick, small-scale informal test of the system may help determine the best way to proceed. In addition, for some systems and attributes, the Level 1 and Level 2 sampling plans may result in oversampling. For example, when one is sampling for identification from the same lot, the suggested levels may result in collecting more samples than are statistically needed; in such cases, the statistically-based sampling plans referenced in Figure 4 can be used.
Sample Collection
Acquiring a representative sample from a lot of bulk powder is a difficult procedure that requires special consideration, and the basic procedures for acquiring a representative sample are discussed below. Note that every situation requires techniques that are appropriate for the given population to be sampled. The methods presented here are applicable to the sampling of static powders stored in midsize bulk containers such as 1-ton super sacks, 50-kg drums, or 50-lb bags. These methods are not necessarily applicable to the sampling of liquids, large storage containers such as train cars or silos, or in-process systems such as blenders or moving conveyer belts. In addition, the procedures described here are most applicable to particles in the size range from approximately ~1 µm to approximately ~1000 µm. Significantly smaller or larger particles require special procedures that are not covered here.
PRIMARY SAMPLE COLLECTION
Lot acceptance samples are generally transferred or delivered in containers. To collect a representative primary or gross sample (see Figure 1), the appropriate container or containers must first be selected from the population of N containers; second, a representative sample must be withdrawn from each of the selected containers.
Container Selection
To avoid bias and other sampling errors, the containers to be sampled must be randomly selected. To make a random selection, first number all containers in the lot, then use a random number table (or computer-generated random numbers) to choose from which container or containers to withdraw the samples.
For systems in which containers are grouped together in such a manner that many of the individual containers are not practically accessible (e.g., 50-lb bags stacked and bound in shrink wrap on a pallet), the sampling plan may need to take into account the larger container, in addition to the smaller container, as a sampling unit, in order to ensure a representative sample.
Withdrawing Sample from a Container
Container Types:
The three most popular container types are the bag, drum, and super sack. Because bags are generally closed and not resealable, special sampling thieves, sometimes called bag triers, have been designed to puncture the bag. If the system to be sampled is heterogeneous, the samples should be obtained from the bottom, center, and top of the bag; and, depending on how the bags are stacked on the pallet, they should also be sampled from the front and the back. When sampling from bags, particular attention should be paid to the corners, because they can disproportionately trap fine particles. If no bag trier is available, use a knife to cut open the bag for sampling. When sampling from a bag, be sure to clean the external surface sufficiently that the sample is not contaminated and foreign material is not introduced into the bulk material. Once the sample has been taken, place a compatible material over the hole in the bag, then fix this patch with an appropriate adhesive tape. Depending on the heterogeneity of the drum, a scoop or a sampling thief is used. Super sacks are large sack containers that usually have a fill spout on the top and a discharge spout on the bottom. For adequately homogeneous material, scoop sampling is appropriate; but if there is any concern about the heterogeneity of the material, a thief should be used. The large size of super sacks makes the use of a thief more important for representative sampling than in the case of a drum or bag, in order to limit potential delimitation error.
Sample Handling
The samples collected can be either assayed individually or combined; then a subset of the gross sample can be assayed, as depicted in Figure 1 and described below. Sample increments should be combined on a clean, dry surface or in a suitable container or bag. All containers with which the sample comes into contact should be inert and should not chemically or physically react with the sample. In addition, samples should be accurately labeled and good records kept. A portion should be kept for possible future analysis.
PRIMARY SAMPLE SIZE REDUCTION
As mentioned above, the primary sample typically consists of multiple samples taken from containers and mixed together. To obtain an analysis or measurement sample (Figure 1), the gross or primary sample must be reduced to a size appropriate for the analytical method. Gross or primary sample size reduction is an often overlooked aspect of a sampling plan, but it is an important step. The factors that cause segregation in a container can also cause segregation in the primary sample, and any bias in the size reduction method for the primary sample will lead to erroneous results. The advantage of secondary samples is that the mass has been reduced to a point at which it is much easer to obtain a representative sample because every element in the powder bed is readily accessible. Such accessibility makes it easier to adhere to sampling best practices. Generally speaking, sample measurement takes place under either wet or dry conditions; the choice is dictated by the requirements of the analytical method. For example, the Coulter counter requires that samples be uniformly suspended in an electrolyte, but other methods, like sieving, are typically performed with dry powders.
Before dividing an agglomerated sample, the agglomerates should be broken apart by a suitable technique such as sieving.
Dry Analysis Methods
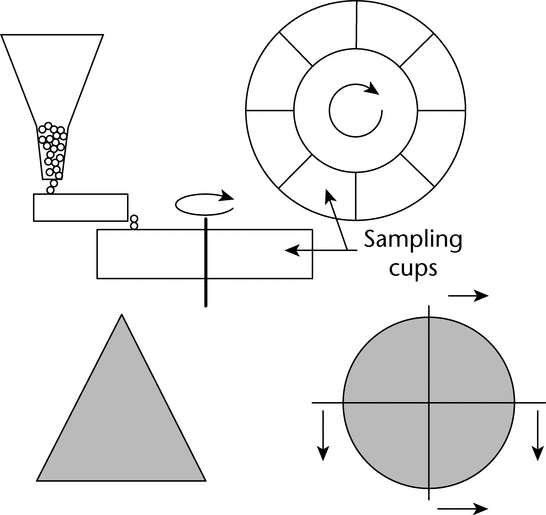
Many laboratory devices are available for the reduction of the primary sample to an analytical sample. The three most important methods used in the pharmaceutical industry are: (1) scoop sampling, (2) cone and quartering, and (3) the spinning riffler or rotary sample divider (manual method of fractional shoveling); see Figure 5.
Figure 5. Two procedures for dividing samples. Top: spinning riffler, in which a circular holder rotates at a constant speed, and the sample is loaded at a constant rate into the containers via a vibratory chute, which is fed by a mass-flow hopper. Bottom: cone and quartering. (Cone, left, is flattened and quartered; quarters can be formed into cones and further subdivided.)
Scoop Sampling:
Scoop sampling is done as previously described, but generally with a smaller scoop or spatula. Great care must be taken when removing material from the primary sample, because this material could be highly segregated as a result of handling. Scoop sampling is appropriate for homogeneous or cohesive powders. However, if the powder is prone to segregation, scoop sampling can introduce significant errors. Moreover, scoop sampling has several serious disadvantages. First, the method depends on the operator’s deciding from which part of the primary sample to scoop the material and what quantity of the sample to extract, which are features that can introduce operator bias. Second, in scoop sampling, operators have a natural tendency to withdraw the sample from the free surface, which is highly prone to segregation and is not representative of the bulk. Third, operators need to avoid creating a heap where rolling segregation can occur, because material could fall off the edges of the spatula or scoop and bias the sample. Ideally, the operator should make some attempt to mix the primary sample before using the scoop, but this too can exacerbate segregation problems and should be done only with great caution.
Cone and Quartering:
Cone and quartering is done by pouring the primary sample into a symmetric cone on a flat surface. The cone is then flattened by a flat surface such as a spatula, and is divided into four identical quarters (Figure 5). One quarter is taken as the sample. This procedure can be repeated (e.g., quarter-samples can be subdivided into quarters) until the desired sample size is obtained. The theory of this method is that when a symmetric cone is created, all the segregation processes also occur symmetrically around the cone, and hence symmetry is used to mitigate the effect of segregation. In practice, it is very difficult to actually make a symmetric powder cone, and the method becomes very operator-dependent and often unreliable. Differences in how operators form the heap and subdivide it can lead to a lack of precision and significant errors. In addition, if the method is done more than once, errors can propagate each time the cone and quartering is performed. Some experts do not recommend this method.
Spinning Riffler:
A spinning riffler (Figure 5) includes a series of containers mounted on a circular holder. The circular holder rotates at a constant speed, and the sample is loaded at a constant rate into the containers via a vibratory chute, which is fed by a mass-flow hopper. Once the material has been divided among the different holders, an individual holder can be removed for testing or further sample division. The angular velocity of the circular holders and the amplitude of the vibratory feeder can be controlled to accommodate powders with different flow properties. The holder velocity and feed rate should be adjusted so that the containers fill uniformly and so that a heap does not form on the vibratory feeder. Spinning rifflers are available in different sizes, making possible subdivisions of powders ranging from a few milligrams to hundreds of grams. The only drawbacks of the spinning riffler are the time required to process the sample and clean the device, and the capital expense. Despite these minor disadvantages, the spinning riffler is by far the best method for subdivision of free-flowing powders.
Fractional shoveling is the manual version of the spinning riffler. In this method, scoop samples are taken from the original sample and placed into a sufficient number of aliquots, and then subsequent scoops are taken from the original sample and placed into one of the aliquots in sequential order. This process is repeated until the original samples are gone. Then one of the aliquots is randomly taken as the reduced sample. As is the case with all manual methods, operator error and variability can be significant factors.
Wet Analysis Methods
Wet analysis methods require dispersing the sample in a liquid suitable for analysis, and then withdrawing an aliquot using a syringe or pipet. Effective secondary sampling requires making a stable homogenous suspension (i.e., the sample must be stable from the time of formation of a suspension to the time when the analysis is complete). Some important factors in wet analysis are sample solubility in the dispersion vehicle, aggregation of sample, the use of suspending agents, and deaggregation of primary particles in the dispersion vehicle. Even though a uniform suspension is created, the sample should be homogenized, typically by shaking, immediately before withdrawing the sample with a syringe or pipet. The diameter of the syringe or pipet should be large enough so that particles are not excluded and clogging does not occur. The diameters of the largest particles should not exceed 40% of the syringe or pipet tip diameter. If for practical reasons the amount of material from the primary sample is too large, the sample size should be reduced before a suspension is made. To reduce the sample size, use the methods described above in the Dry Analysis Methods section. As a precaution, collect and retain enough sample to repeat all tests a minimum of five times.
APPENDIX 1: SUBSAMPLING EXAMPLES
The examples provided below describe the importance of material particle characterization during the selection of an appropriate sample mass. Four examples are presented. In the first example, similarity in the fundamental or intrinsic material characteristics is assumed. In the second example, the density of the heavy metal analyte being measured is changed. In the third example, the effect of changing the particle size is evaluated. In the fourth example, the adequacy of the fundamental particle characteristics in a formulation needed for a given unit dose or mass is evaluated.
Example 1. Sample Mass Determination
Assuming the lot size is 1 kg, the maximum particle diameter is 1000 µm, and the concentration of the analyte is expected to be 1%, what sample mass of round, equal-sized and -shaped 1000-µm particles with a density of 1 g/cm3 would be needed to estimate the average concentration of the analyte with a percent relative standard deviation (%RSD) of 5%?
Rearranging equation 3, one can estimate the sample mass as shown in equation 5:
The compositional maximum heterogeneity (cmax) can be estimated by considering the analyte and matrix density (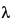 a and
a and 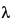 m, respectively, and their average
m, respectively, and their average 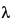 ) and analyte concentration (aL) (equation 6):
) and analyte concentration (aL) (equation 6):
For low analyte concentrations, the compositional maximum heterogeneity is simplified to equation 7:
For high analyte concentrations, the compositional maximum heterogeneity is simplified to equation 8:
The shape factor is approximated by equation 9:
Where d is the nominal particle diameter for a sphere, and the shape factor is [(4/3)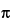 /8], or approximately 0.5.
/8], or approximately 0.5.
The granulometric factor can be approximated by the typical minimum diameter noted as the 5th percentile size, divided by the typical maximum diameter noted as the 95th percentile size, as shown in equation 10:
Because all particles are the same size, the granulometric factor, gCF, is 1.0. Because the analyte exists in a state liberated from the matrix particles, the liberation factor is also 1.0. The sample mass for a 5% RSD (using equation 5) is then:
A sample mass of 19.6 g will provide a sampling error of approximately 5% RSD. Note that in this example the particle characteristics are simplified to demonstrate that a lot mass of 1000 g contains 2 × 106 particles of 0.5 mg mass. The sample mass of 19.6 g contains approximately 39,216 particles, yielding a 5% RSD, using the binomial distribution where p is the concentration of the analyte (aL) and n is the number of particles sampled, as shown in equation 11.
(See Table 2 for a summary of calculations.)
Table 2. Summary of Calculations for Example 1, Equal-Sized and -Shaped Particles
| mLot (g) | d (cm) | fshape | gCF | cmax | aL | l | ms (g) | |
|---|---|---|---|---|---|---|---|---|
| 1000 | 0.1 | 0.5 | 1 | 100.0 | 0.01 | 1 | 1 | 19.6 |
| Mass per Particle Ps
d3fshape |
Particles in 19.6 g ms/(Ps/gCF) |
Binomial RSD p = a(L) = 0.01 n = 39,216 (Eq. 11) |
||||||
| 0.005 | 39,216 | 0.05 | ||||||
In determining the required sample mass, it is assumed that the sample is representative of the population. Moreover, when using a single representative sample, it is assumed that the uniformity of the sample mass is consistent with the remaining population. Note that the granulometric and liberation factors allow proportional adjustment of the sample size, depending on the nature of the particles. The inclusion of a liberation factor in the equation allows for particles to exist with a proportion of the analyte residing within every particle or a proportion thereof. The granulometric factor permits adjustment of the sample mass by accounting for the relationship in size between the smallest and largest particles represented in the lot.
This approximation also can be applied to liquid suspensions in which each particle is considered discrete and the sample can be characterized with respect to size, density, mass, and volume.
Example 2. Heavy Metal
In this example, it is assumed that the analyte is the heavy metal lead, with a density of 11.34 g/cm3, with a limit of not more than 5 ppm, where the shapes of the particles are cubes (fshape = 1.0), the particles are approximately 50 µm, and a 5-g sample is taken from screened material (gCF = 0.55). On the basis of equation 3, the %RSD is 17.7%. Using equation 5, one finds that a sample mass of approximately 60 g is needed to achieve a 5% RSD, assuming that aL is equal to the limit allowed and that the analyte cannot be assumed to be liberated from the material (l = 1.0). (See Table 3 for a summary of calculations.)
Table 3. Summary of Calculations for Example 2, Heavy Metal
| mLot (g) | d (cm) | fshape | gCF | cmax | aL | l | mS (g) | |
|---|---|---|---|---|---|---|---|---|
| 1000 | 0.005 | 1.0 | 0.55 | 2.3 × 106 | 5 × 10 |
11.34 | 1.0 | 58.71 |
If the sample were assumed to be homogeneous (l = 0.1) with respect to presence of the analyte with all particles, then a sample mass of 6.2 g would be required. Moreover, if the shape of the particles were between round and cubic (fshape = 0.8), then a sample mass of 5 g would be required to complete the analysis.
Example 3. Subsampling
Ideal sampling, as noted earlier, is fundamental to understanding the important role of subsampling. In many instances it is desirable to reduce the sample size in a manner that results in a representative sample and lessens the need to test a large sample mass. In some cases the particle size and compositional heterogeneity can result in an unwieldy sample mass. This may occur with larger-sized particles or when a composite sample of many containers is required. Samples with larger-sized particles may need to be physically reduced.
For example, using Example 2 above, if the maximum particle size were 1000 µm or 1 mm, then a 997-g sample would be suggested by equation 3. Reducing the particle size by grinding and subsampling to achieve a predetermined sampling %RSD may require subsampling more than once to achieve the desired particle size. For example, the entire sample may be reduced to 100 µm to reduce the %RSD to approximately 3%; then, with ideal sampling, a subsample could be selected and entirely reduced to 50 µm to achieve a 5% RSD. Finally, a 5-g subsample could be correctly taken and tested. If certain particles have a large size with high concentration of the analyte, then samples should be selected to ensure that at least 1, but preferably at least 5–6, particles would be selected with 95% probability or chance of selection.
Example 4. Minimum Unit Dosage Mass
A formulator would like to know the minimum mass required for a dosage form to ensure with 95% confidence a unit dosage of 1% active drug powder. The drug and the excipient have a similar round shape (fshape = 0.5) and a density of 0.33 g/cm3. The active drug is milled to 1 µm, but the size of excipients can be as large as 200 µm. The value for gCF is taken from equation 10 using the expected range of the excipient that accounts for 95% of the formulation, as 10 µm/200 µm, or gCF = 0.05. The quantity cmax from equation 7 is taken as 0.33/0.01. The drug particles are completely liberated from the excipient. The batch size is 100 kg.
Table 4. Summary of Calculations for Example 4, Minimum Unit Dose Mass
| mLot (g) | d (cm) | fshape | gCF | cmax | aL | l | mS (g) | |
|---|---|---|---|---|---|---|---|---|
| 105 | 0.02 | 0.5 | 0.05 | 33 | 0.01 | 0.33 | 1.0 | 0.00264 |
A minimum sample mass of approximately 3 mg is needed to ensure with 95% confidence (2 RSDs) that the average drug content is 0.9%–1.1%. The proposed dosage form has an active concentration of 100 µm/10 mg total unit mass. The unit dosage form mass is adequate, but the formulation requires that the mixing process, unit dosage production, bulk sampling device, and lab sample preparation or subsampling from bulk samples result in equal probability of selection of drug particles. Only if these conditions for mixing, production, sampling, and testing are met can it be reliably demonstrated that the unit dosage and test determination acceptance criteria of 1% (0.01 µg/mg) are met. Acceptable outcomes of such testing also indicate that the particle size, shape, and density must be controlled. For example, an increase in the sizes of particles to 500 µm results in a need for a 42-mg sample mass and dose. Assuming a cubic, as opposed to a rounded, particle increases the sample mass to 5 mg, which for a fixed dosage form mass may result in less room for the variation contributed by other characteristics, or in lesser confidence. If the acceptance criteria were changed to 0.95%–1.05%, requiring a 1% RSD, then the minimum sample mass would increase to approximately 70 mg. (See Table 4 for a summary of calculations.)
APPENDIX 2: MATERIAL CHARACTERIZATION AND SAMPLING
Specific and thorough knowledge of the material’s synthesis, composition, and usage is critical to developing a bulk material sampling plan. Material characterization is important because bulk material can exist in many forms throughout the material process flow. As illustrated in Figure 6, the type of sampling can vary by process step and ultimately affects the use of the material in the drug product. Appropriate material characterization considers the material process step, the type of sampling, the objective of the process step, and ultimately the drug product.
For example, material can be synthesized or mixed in a large container where sampling may be limited or ideal for the characteristic needed. If the characteristic is important but the sampling conditions are not ideal, perhaps because of the heterogeneity of a powder mixture, then sampling for that characteristic may be more appropriately performed at a different stage upstream or downstream to assess the heterogeneity of the contents and ensure ideal sampling. This is sometimes performed to reduce the sampling dimension. The sampling dimension is reduced when the 3 dimensional bulk container space is sampled in a 1 or 2 dimensional stream sampled over time. Reducing the spatial sampling dimension may result in conditions that will allow for more accurate measurement of the heterogeneity of material while limiting sampling error through ideal sampling.
Acceptance attributes (see Table 5) depend on material characterization and process. Acceptance attributes may be applicable throughout the life of the bulk material. Both the number and size of samples require an understanding of the material's variation.
Table 5. Examples of Acceptance Attributes
| Acceptance Attributes | |||
|---|---|---|---|
| Physical | Chemical | Microbiological | Packaging |
| Particle size Viscosity Density |
Purity pH Identity Strength |
Sterility Pyrogens Microbial load |
Label accuracy Integrity |
APPENDIX 3: ADDITIONAL SOURCES OF INFORMATION
- Allen, T, Particle Size Measurement, 5th ed., Vol. 1, Powder Technology Series, B. Scarlett and G. Jimbo (Eds.), 1997, London: Chapman & Hall, p. 525.
- Beebe, KR, RJ Pell, and MB Seasholtz, Chemometrics: A Practical Guide. 1998, New York: John Wiley & Sons, p. 348.
- Brereton, RG, Chemometrics Data Analysis for the Laboratory and Chemical Plant. 2003, Chichester, England: John Wiley & Sons, p. 489.
- Burns, DA, and EW Ciurczak, Handbook of Near-Infrared Analysis: Practical Spectroscopy, 2nd ed. 1992, New York: Marcel Dekker.
- Chowhan, Z, Segregation of particulate solids, Part 1. Pharm. Technol., 1995, 19(May): pp. 56, 58, 60, 62, 64, 66, 68, 70.
- Chowhan, Z, Segregation of particulate solids, Part 2. Pharm. Technol., 1995, 19(June): pp. 80, 82, 84, 86, 88, 90, 92, 94.
- Gerlach, RW, and JM Nocerino, Guidance for Obtaining Representative Laboratory Analytical Subsamples from Particulate Laboratory Samples. U.S. Environmental Protection Agency EPA/600/R-03/027, November 2003.
- Jillavenkatesa, A, SJ Dapkunas, and L-SH Lum, Particle Size Characterization, Special Publication 960-1, National Institute for Science and Technology, 2001.
- Kramer, R, ed., Chemometric Techniques for Quantitative Analysis. 1998, New York: Marcel Dekker, p. 203.
- Malinowski, ER, Factor Analysis in Chemistry, 3rd ed. 2002, New York: John Wiley and Sons, p. 414.
- Martens, H, and T Naes, Multivaritate Calibration. 1989, Chichester, England: John Wiley & Sons, p. 419.
- Muzzio, F, et al., Sampling and characterization of pharmaceutical powders and granular blends. Int. J. Pharm., 2003, 250(1): pp. 51–64.
- Muzzio, FJ, et al., Sampling practices in powder blending. Int. J. Pharm., 1997, 155(2): pp. 153–178.
- Petersen, L, CK Dahl, and KH Esbensen, Representative mass reduction in sampling—a critical survey of techniques and hardware. Chemom. Intell. Lab. Syst., 2004, 74: pp. 95–114.
- Petersen, L, P Minkkinen, and KH Esbensen, Representative sampling for reliable data analysis: theory of sampling. Chemom. Intell. Lab. Syst., 2005, 77: pp. 261–277.
- Sastry, KVS, et al., Solid-solid operation and equipment, in Perry's Chemical Engineeer's Handbook, RH Perry, DW Green, and JO Maloney, Eds. 1997, New York: McGraw-Hill, pp. 19-1–19-65.
- Skoog, DA, and JJ Leary, Principles of Instrumental Analysis, 4th ed. 1992, Fort Worth, TX: Saunders College Publishing, p. 700.
- Smith, PL, A Primer for Sampling Solids, Liquids, and Gases: Based on the Seven Sampling Errors of Pierre Gy. In ASA-SIAM Series on Statistics and Applied Probability, RF Gunst, ed. 2001, Philadelphia: Society for Industrial & Applied Mathematics. p. 96.
- Tatavarti, AS, et al., Assessment of NIR spectroscopy for nondestructive analysis of physical and chemical attributes of sulfamethazine bolus dosage forms. AAPS PharmSciTech, 2005, 6(1): pp. E91–E99.
- Venables, H, and J Wells, Powder sampling. Drug Dev. Ind. Pharm., 2002, 28(2): pp. 107–117.
Auxiliary Information—
Please check for your question in the FAQs before contacting USP.
| Topic/Question | Contact | Expert Committee |
|---|---|---|
| General Chapter | Horacio N. Pappa, Ph.D.
Principal Scientific Liaison 1-301-816-8319 |
(STAT2010) Statistics 2010 |
USP35–NF30 Page 681
Pharmacopeial Forum: Volume No. 36(3) Page 760