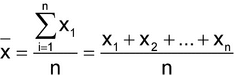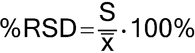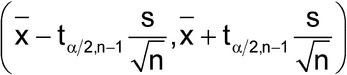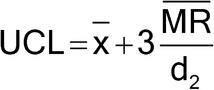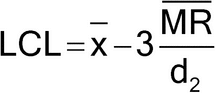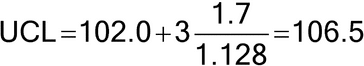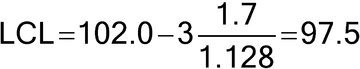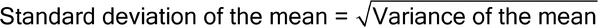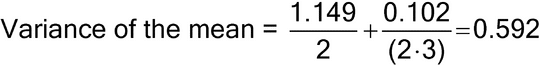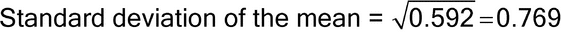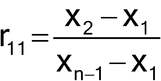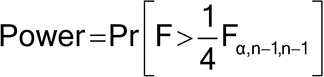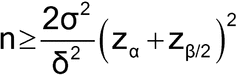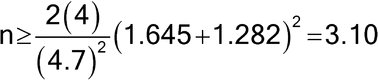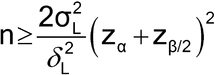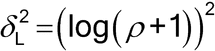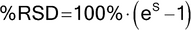1010 ANALYTICAL DATA—INTERPRETATION AND TREATMENT

INTRODUCTION
This chapter provides information regarding acceptable practices for the analysis and consistent interpretation of data obtained from chemical and other analyses. Basic statistical approaches for evaluating data are described, and the treatment of outliers and comparison of analytical methods are discussed in some detail.
NOTE—It should not be inferred that the analysis tools mentioned in this chapter form an exhaustive list. Other, equally valid, statistical methods may be used at the discretion of the manufacturer and other users of this chapter.
Assurance of the quality of pharmaceuticals is accomplished by combining a number of practices, including robust formulation design, validation, testing of starting materials, in-process testing, and final-product testing. Each of these practices is dependent on reliable test methods. In the development process, test procedures are developed and validated to ensure that the manufactured products are thoroughly characterized. Final-product testing provides further assurance that the products are consistently safe, efficacious, and in compliance with their specifications.
Measurements are inherently variable. The variability of biological tests has long been recognized by the USP. For example, the need to consider this variability when analyzing biological test data is addressed under Design and Analysis of Biological Assays 111. The chemical analysis measurements commonly used to analyze pharmaceuticals are also inherently variable, although less so than those of the biological tests. However, in many instances the acceptance criteria are proportionally tighter, and thus, this smaller allowable variability has to be considered when analyzing data generated using analytical procedures. If the variability of a measurement is not characterized and stated along with the result of the measurement, then the data can only be interpreted in the most limited sense. For example, stating that the difference between the averages from two laboratories when testing a common set of samples is 10% has limited interpretation, in terms of how important such a difference is, without knowledge of the intralaboratory variability.
This chapter provides direction for scientifically acceptable treatment and interpretation of data. Statistical tools that may be helpful in the interpretation of analytical data are described. Many descriptive statistics, such as the mean and standard deviation, are in common use. Other statistical tools, such as outlier tests, can be performed using several different, scientifically valid approaches, and examples of these tools and their applications are also included. The framework within which the results from a compendial test are interpreted is clearly outlined in Test Results, Statistics, and Standards under General Notices and Requirements. Selected references that might be helpful in obtaining additional information on the statistical tools discussed in this chapter are listed in Appendix F at the end of the chapter. USP does not endorse these citations, and they do not represent an exhaustive list. Further information about many of the methods cited in this chapter may also be found in most statistical textbooks.

PREREQUISITE LABORATORY PRACTICES AND PRINCIPLES
The sound application of statistical principles to laboratory data requires the assumption that such data have been collected in a traceable (i.e., documented) and unbiased manner. To ensure this, the following practices are beneficial.
Sound Record Keeping
Laboratory records are maintained with sufficient detail, so that other equally qualified analysts can reconstruct the experimental conditions and review the results obtained. When collecting data, the data should generally be obtained with more decimal places than the specification requires and rounded only after final calculations are completed as per the General Notices and Requirements.
Sampling Considerations
Effective sampling is an important step in the assessment of a quality attribute of a population. The purpose of sampling is to provide representative data (the sample) for estimating the properties of the population. How to attain such a sample depends entirely on the question that is to be answered by the sample data. In general, use of a random process is considered the most appropriate way of selecting a sample. Indeed, a random and independent sample is necessary to ensure that the resulting data produce valid estimates of the properties of the population. Generating a nonrandom or “convenience” sample risks the possibility that the estimates will be biased. The most straightforward type of random sampling is called simple random sampling, a process in which every unit of the population has an equal chance of appearing in the sample. However, sometimes this method of selecting a random sample is not optimal because it cannot guarantee equal representation among factors (i.e., time, location, machine) that may influence the critical properties of the population. For example, if it requires 12 hours to manufacture all of the units in a lot and it is vital that the sample be representative of the entire production process, then taking a simple random sample after the production has been completed may not be appropriate because there can be no guarantee that such a sample will contain a similar number of units made from every time period within the 12-hour process. Instead, it is better to take a systematic random sample whereby a unit is randomly selected from the production process at systematically selected times or locations (e.g., sampling every 30 minutes from the units produced at that time) to ensure that units taken throughout the entire manufacturing process are included in the sample. Another type of random sampling procedure is needed if, for example, a product is filled into vials using four different filling machines. In this case it would be important to capture a random sample of vials from each of the filling machines. A stratified random sample, which randomly samples an equal number of vials from each of the four filling machines, would satisfy this requirement. Regardless of the reason for taking a sample (e.g., batch-release testing), a sampling plan should be established to provide details on how the sample is to be obtained to ensure that the sample is representative of the entirety of the population and that the resulting data have the required sensitivity. The optimal sampling strategy will depend on knowledge of the manufacturing and analytical measurement processes. Once the sampling scheme has been defined, it is likely that the sampling will include some element of random selection. Finally, there must be sufficient sample collected for the original analysis, subsequent verification analyses, and other analyses. Consulting a statistician to identify the optimal sampling strategy is recommended.
Tests discussed in the remainder of this chapter assume that simple random sampling has been performed.
Use of Reference Standards
Where the use of the USP Reference Standard is specified, the USP Reference Standard, or a secondary standard traceable to the USP Reference Standard, is used. Because the assignment of a value to a standard is one of the most important factors that influences the accuracy of an analysis, it is critical that this be done correctly.
System Performance Verification
Verifying an acceptable level of performance for an analytical system in routine or continuous use can be a valuable practice. This may be accomplished by analyzing a control sample at appropriate intervals, or using other means, such as, variation among the standards, background signal-to-noise ratios, etc. Attention to the measured parameter, such as charting the results obtained by analysis of a control sample, can signal a change in performance that requires adjustment of the analytical system. An example of a controlled chart is provided in Appendix A.
Method Validation
All methods are appropriately validated as specified under Validation of Compendial Procedures 1225. Methods published in the USP–NF have been validated and meet the Current Good Manufacturing Practices regulatory requirement for validation as established in the Code of Federal Regulations. A validated method may be used to test a new formulation (such as a new product, dosage form, or process intermediate) only after confirming that the new formulation does not interfere with the accuracy, linearity, or precision of the method. It may not be assumed that a validated method could correctly measure the active ingredient in a formulation that is different from that used in establishing the original validity of the method. [Note on terminology—The definition of accuracy in Validation of Compendial Procedures 1225 and in ICH Q2 corresponds to unbiasedness only. In the International Vocabulary of Metrology (VIM) and documents of the International Organization for Standardization (ISO), accuracy has a different meaning. In ISO, accuracy combines the concepts of unbiasedness (termed trueness) and precision. This chapter follows the definition in chapter 1225, which corresponds only to trueness. ]

MEASUREMENT PRINCIPLES AND VARIATION
All measurements are, at best, estimates of the actual (“true” or “accepted”) value for they contain random variability (also referred to as random error) and may also contain systematic variation (bias). Thus, the measured value differs from the actual value because of variability inherent in the measurement. If an array of measurements consists of individual results that are representative of the whole, statistical methods can be used to estimate informative properties of the entirety, and statistical tests are available to investigate whether it is likely that these properties comply with given requirements. The resulting statistical analyses should address the variability associated with the measurement process as well as that of the entity being measured. Statistical measures used to assess the direction and magnitude of these errors include the mean, standard deviation, and expressions derived therefrom, such as the percent coefficient of variation (%CV, also called the percent relative standard deviation, %RSD). The estimated variability can be used to calculate confidence intervals for the mean, or measures of variability, and tolerance intervals capturing a specified proportion of the individual measurements.
The use of statistical measures must be tempered with good judgment, especially with regard to representative sampling. Data should be consistent with the statistical assumptions used for the analysis. If one or more of these assumptions appear to be violated, alternative methods may be required in the evaluation of the data. In particular, most of the statistical measures and tests cited in this chapter rely on the assumptions that the distribution of the entire population is represented by a normal distribution and that the analyzed sample is a representative subset of this population. The normal (or Gaussian) distribution is bell-shaped and symmetric about its center and has certain characteristics that are required for these tests to be valid. The data may not always be expected to be normally distributed and may require a transformation to better fit a normal distribution. For example, there exist variables that have distributions with longer right tails than left. Such distributions can often be made approximately normal through a log transformation. An alternative approach would be to use “distribution-free” or “nonparametric” statistical procedures that do not require that the shape of the population be that of a normal distribution. When the objective is to construct a confidence interval for the mean or for the difference between two means, for example, then the normality assumption is not as important because of the central limit theorem. However, one must verify normality of data to construct valid confidence intervals for standard deviations and ratios of standard deviations, perform some outlier tests, and construct valid statistical tolerance limits. In the latter case, normality is a critical assumption. Simple graphical methods, such as dot plots, histograms, and normal probability plots, are useful aids for investigating this assumption.
A single analytical measurement may be useful in quality assessment if the sample is from a whole that has been prepared using a well-validated, documented process and if the analytical errors are well known. The obtained analytical result may be qualified by including an estimate of the associated errors. There may be instances when one might consider the use of averaging because the variability associated with an average value is always reduced as compared to the variability in the individual measurements. The choice of whether to use individual measurements or averages will depend upon the use of the measure and its variability. For example, when multiple measurements are obtained on the same sample aliquot, such as from multiple injections of the sample in an HPLC method, it is generally advisable to average the resulting data for the reason discussed above.
Variability is associated with the dispersion of observations around the center of a distribution. The most commonly used statistic to measure the center is the sample mean (x):
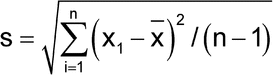
Click to View Image
Method variability can be estimated in various ways. The most common and useful assessment of a method's variability is the determination of the standard deviation based on repeated independent1 measurements of a sample. The sample standard deviation, s, is calculated by the formula:
Click to View Image
in which xI is the individual measurement in a set of n measurements; and x is the mean of all the measurements. The percent relative standard deviation (%RSD) is then calculated as:
Click to View Image
and expressed as a percentage. If the data requires log transformation to achieve normality (e.g., for biological assays), then alternative methods are available.2
A precision study should be conducted to provide a better estimate of method variability. The precision study may be designed to determine intermediate precision (which includes the components of both “between run” and “within-run” variability) and repeatability (“within-run” variability). The intermediate precision studies should allow for changes in the experimental conditions that might be expected, such as different analysts, different preparations of reagents, different days, and different instruments. To perform a precision study, the test is repeated several times. Each run must be completely independent of the others to provide accurate estimates of the various components of variability. In addition, within each run, replicates are made in order to estimate repeatability. See an example of a precision study under Appendix B.
A confidence interval for the mean may be considered in the interpretation of data. Such intervals are calculated from several data points using the sample mean (x) and sample standard deviation(s) according to the formula:
Click to View Image
in which t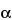/2,n–1 is a statistical number dependent upon the sample size (n), the number of degrees of freedom (n – 1), and the desired confidence level (1 – 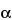). Its values are obtained from published tables of the Student t-distribution. The confidence interval provides an estimate of the range within which the “true” population mean (µ) falls, and it also evaluates the reliability of the sample mean as an estimate of the true mean. If the same experimental set-up were to be replicated over and over and a 95% (for example) confidence interval for the true mean is calculated each time, then 95% of such intervals would be expected to contain the true mean, µ. One cannot say with certainty whether or not the confidence interval derived from a specific set of data actually collected contains µ. However, assuming the data represent mutually independent measurements randomly generated from a normally distributed population, the procedure used to construct the confidence interval guarantees that 95% of such confidence intervals contain µ. Note that it is important to define the population appropriately so that all relevant sources of variation are captured. [Note on terminology—In the documents of the International Organization for Standardization (ISO), different terminology is used for some of the concepts described here. The term s/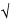n, which is commonly called the standard error of the mean, is called the standard uncertainty in ISO documents. The term t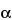/2,n1 S/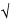n is called the expanded uncertainty, and t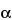/2,n 1 is called the coverage factor, by ISO. If the standard deviation is found by combining estimates of variability from multiple sources, it is called the combined standard uncertainty. Some of these sources could have nonstatistical estimates of uncertainty, called Type B uncertainties, such as uncertainty in calibration of a balance. ]

OUTLYING RESULTS
Occasionally, observed analytical results are very different from those expected. Aberrant, anomalous, contaminated, discordant, spurious, suspicious or wild observations; and flyers, rogues, and mavericks are properly called outlying results. Like all laboratory results, these outliers must be documented, interpreted, and managed. Such results may be accurate measurements of the entity being measured, but are very different from what is expected. Alternatively, due to an error in the analytical system, the results may not be typical, even though the entity being measured is typical. When an outlying result is obtained, systematic laboratory and process investigations of the result are conducted to determine if an assignable cause for the result can be established. Factors to be considered when investigating an outlying result include—but are not limited to—human error, instrumentation error, calculation error, and product or component deficiency. If an assignable cause that is not related to a product or component deficiency can be identified, then retesting may be performed on the same sample, if possible, or on a new sample. The precision and accuracy of the method, the Reference Standard, process trends, and the specification limits should all be examined. Data may be invalidated, based on this documented investigation, and eliminated from subsequent calculations.
If no documentable, assignable cause for the outlying laboratory result is found, the result may be tested, as part of the overall investigation, to determine whether it is an outlier.
However, careful consideration is warranted when using these tests. Two types of errors may occur with outlier tests: (a) labeling observations as outliers when they really are not; and (b) failing to identify outliers when they truly exist. Any judgment about the acceptability of data in which outliers are observed requires careful interpretation.
“Outlier labeling” is informal recognition of suspicious laboratory values that should be further investigated with more formal methods. The selection of the correct outlier identification technique often depends on the initial recognition of the number and location of the values. Outlier labeling is most often done visually with graphical techniques. “Outlier identification” is the use of statistical significance tests to confirm that the values are inconsistent with the known or assumed statistical model.
When used appropriately, outlier tests are valuable tools for pharmaceutical laboratories. Several tests exist for detecting outliers. Examples illustrating three of these procedures, the Extreme Studentized Deviate (ESD) Test, Dixon's Test, and Hampel's Rule, are presented in Appendix C.
Choosing the appropriate outlier test will depend on the sample size and distributional assumptions. Many of these tests (e.g., the ESD Test) require the assumption that the data generated by the laboratory on the test results can be thought of as a random sample from a population that is normally distributed, possibly after transformation. If a transformation is made to the data, the outlier test is applied to the transformed data. Common transformations include taking the logarithm or square root of the data. Other approaches to handling single and multiple outliers are available and can also be used. These include tests that use robust measures of central tendency and spread, such as the median and median absolute deviation and exploratory data analysis (EDA) methods. “Outlier accommodation” is the use of robust techniques, such as tests based on the order or rank of each data value in the data set instead of the actual data value, to produce results that are not adversely influenced by the presence of outliers. The use of such methods reduces the risks associated with both types of error in the identification of outliers.
“Outlier rejection” is the actual removal of the identified outlier from the data set. However, an outlier test cannot be the sole means for removing an outlying result from the laboratory data. An outlier test may be useful as part of the evaluation of the significance of that result, along with other data. Outlier tests have no applicability in cases where the variability in the product is what is being assessed, such as content uniformity, dissolution, or release-rate determination. In these applications, a value determined to be an outlier may in fact be an accurate result of a nonuniform product. All data, especially outliers, should be kept for future review. Unusual data, when seen in the context of other historical data, are often not unusual after all but reflect the influences of additional sources of variation.
In summary, the rejection or retention of an apparent outlier can be a serious source of bias. The nature of the testing as well as scientific understanding of the manufacturing process and analytical method have to be considered to determine the source of the apparent outlier. An outlier test can never take the place of a thorough laboratory investigation. Rather, it is performed only when the investigation is inconclusive and no deviations in the manufacture or testing of the product were noted. Even if such statistical tests indicate that one or more values are outliers, they should still be retained in the record. Including or excluding outliers in calculations to assess conformance to acceptance criteria should be based on scientific judgment and the internal policies of the manufacturer. It is often useful to perform the calculations with and without the outliers to evaluate their impact.
Outliers that are attributed to measurement process mistakes should be reported (i.e., footnoted), but not included in further statistical calculations. When assessing conformance to a particular acceptance criterion, it is important to define whether the reportable result (the result that is compared to the limits) is an average value, an individual measurement, or something else. If, for example, the acceptance criterion was derived for an average, then it would not be statistically appropriate to require individual measurements to also satisfy the criterion because the variability associated with the average of a series of measurements is smaller than that of any individual measurement.

COMPARISON OF ANALYTICAL METHODS
It is often necessary to compare two methods to determine if their average results or their variabilities differ by an amount that is deemed important. The goal of a method comparison experiment is to generate adequate data to evaluate the equivalency of the two methods over a range of concentrations. Some of the considerations to be made when performing such comparisons are discussed in this section.
Precision
Precision is the degree of agreement among individual test results when the analytical method is applied repeatedly to a homogeneous sample. For an alternative method to be considered to have “comparable” precision to that of a current method, its precision (see Analytical Performance Characteristics under Validation of Compendial Procedures 1225) must not be worse than that of the current method by an amount deemed important. A decrease in precision (or increase in variability) can lead to an increase in the number of results expected to fail required specifications. On the other hand, an alternative method providing improved precision is acceptable.
One way of comparing the precision of two methods is by estimating the variance for each method (the sample variance, s2, is the square of the sample standard deviation) and calculating a one-sided upper confidence interval for the ratio of (true) variances, where the ratio is defined as the variance of the alternative method to that of the current method. An example, with this assumption, is outlined under Appendix D. The one-sided upper confidence limit should be compared to an upper limit deemed acceptable, a priori, by the analytical laboratory. If the one-sided upper confidence limit is less than this upper acceptable limit, then the precision of the alternative method is considered acceptable in the sense that the use of the alternative method will not lead to an important loss in precision. Note that if the one-sided upper confidence limit is less than one, then the alternative method has been shown to have improved precision relative to the current method.
The confidence interval method just described is preferred to applying the two-sample F-test to test the statistical significance of the ratio of variances. To perform the two-sample F-test, the calculated ratio of sample variances would be compared to a critical value based on tabulated values of the F distribution for the desired level of confidence and the number of degrees of freedom for each variance. Tables providing F-values are available in most standard statistical textbooks. If the calculated ratio exceeds this critical value, a statistically significant difference in precision is said to exist between the two methods. However, if the calculated ratio is less than the critical value, this does not prove that the methods have the same or equivalent level of precision; but rather that there was not enough evidence to prove that a statistically significant difference did, in fact, exist.
Accuracy
Comparison of the accuracy (see Analytical Performance Characteristics under Validation of Compendial Procedures 1225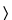) of methods provides information useful in determining if the new method is equivalent, on the average, to the current method. A simple method for making this comparison is by calculating a confidence interval for the difference in true means, where the difference is estimated by the sample mean of the alternative method minus that of the current method.
The confidence interval should be compared to a lower and upper range deemed acceptable, a priori, by the laboratory. If the confidence interval falls entirely within this acceptable range, then the two methods can be considered equivalent, in the sense that the average difference between them is not of practical concern. The lower and upper limits of the confidence interval only show how large the true difference between the two methods may be, not whether this difference is considered tolerable. Such an assessment can be made only within the appropriate scientific context.
The confidence interval method just described is preferred to the practice of applying a t-test to test the statistical significance of the difference in averages. One way to perform the t-test is to calculate the confidence interval and to examine whether or not it contains the value zero. The two methods have a statistically significant difference in averages if the confidence interval excludes zero. A statistically significant difference may not be large enough to have practical importance to the laboratory because it may have arisen as a result of highly precise data or a larger sample size. On the other hand, it is possible that no statistically significant difference is found, which happens when the confidence interval includes zero, and yet an important practical difference cannot be ruled out. This might occur, for example, if the data are highly variable or the sample size is too small. Thus, while the outcome of the t-test indicates whether or not a statistically significant difference has been observed, it is not informative with regard to the presence or absence of a difference of practical importance.
Determination of Sample Size
Sample size determination is based on the comparison of the accuracy and precision of the two methods3 and is similar to that for testing hypotheses about average differences in the former case and variance ratios in the latter case, but the meaning of some of the input is different. The first component to be specified is , the largest acceptable difference between the two methods that, if achieved, still leads to the conclusion of equivalence. That is, if the two methods differ by no more than , on the average, they are considered acceptably similar. The comparison can be two-sided as just expressed, considering a difference of in either direction, as would be used when comparing means. Alternatively, it can be one-sided as in the case of comparing variances where a decrease in variability is acceptable and equivalency is concluded if the ratio of the variances (new/current, as a proportion) is not more than 1.0 + . A researcher will need to state based on knowledge of the current method and/or its use, or it may be calculated. One consideration, when there are specifications to satisfy, is that the new method should not differ by so much from the current method as to risk generating out-of-specification results. One then chooses to have a low likelihood of this happening by, for example, comparing the distribution of data for the current method to the specification limits. This could be done graphically or by using a tolerance interval, an example of which is given in Appendix E. In general, the choice for must depend on the scientific requirements of the laboratory.
The next two components relate to the probability of error. The data could lead to a conclusion of similarity when the methods are unacceptably different (as defined by ). This is called a false positive or Type I error. The error could also be in the other direction; that is, the methods could be similar, but the data do not permit that conclusion. This is a false negative or Type II error. With statistical methods, it is not possible to completely eliminate the possibility of either error. However, by choosing the sample size appropriately, the probability of each of these errors can be made acceptably small. The acceptable maximum probability of a Type I error is commonly denoted as 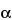and is commonly taken as 5%, but may be chosen differently. The desired maximum probability of a Type II error is commonly denoted by 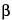. Often, 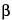is specified indirectly by choosing a desired level of 1 – 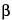, which is called the “power” of the test. In the context of equivalency testing, power is the probability of correctly concluding that two methods are equivalent. Power is commonly taken to be 80% or 90% (corresponding to a 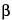of 20% or 10%), though other values may be chosen. The protocol for the experiment should specify , , 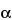and power. The sample size will depend on all of these components. An example is given in Appendix E. Although Appendix E determines only a single value, it is often useful to determine a table of sample sizes corresponding to different choices of , , 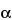and power. Such a table often allows for a more informed choice of sample size to better balance the competing priorities of resources and risks (false negative and false positive conclusions).

APPENDIX A: CONTROL CHARTS
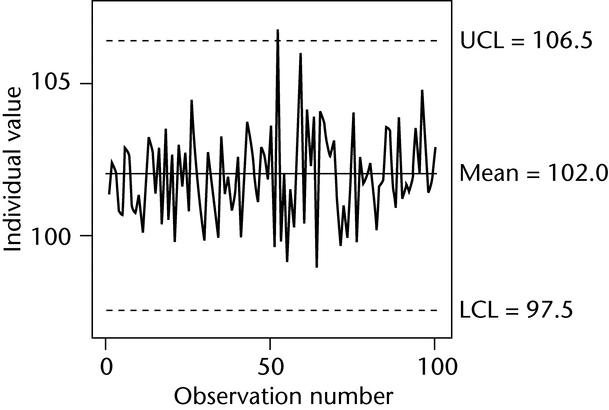
Figure 1 illustrates a control chart for individual values. There are several different methods for calculating the upper control limit (UCL) and lower control limit (LCL). One method involves the moving range, which is defined as the absolute difference between two consecutive measurements (|xi – xI–1|). These moving ranges are averaged ( MR ) and used in the following formulas:
Click to View Image
Click to View Image
where x is the sample mean, and d2 is a constant commonly used for this type of chart and is based on the number of observations associated with the moving range calculation. Where n = 2 (two consecutive measurements), as here, d2 = 1.128. For the example in Figure 1, the MR was 1.7:
Click to View Image
Click to View Image
Other methods exist that are better able to detect small shifts in the process mean, such as the cumulative sum (also known as “CUSUM”) and exponentially weighted moving average (“EWMA”).
Click to View Image
Figure 1. Individual X or individual measurements control chart for control samples. In this particular example, the mean for all the samples (x) is 102.0, the UCL is 106.5, and the LCL is 97.5.

APPENDIX B: PRECISION STUDY
Table 1 displays data collected from a precision study. This study consisted of five independent runs and, within each run, results from three replicates were collected.
Performing an analysis of variance (ANOVA) on the data in Table 1 leads to the ANOVA table (Table 1A). Because there were an equal number of replicates per run in the precision study, values for VarianceRun and VarianceRep can be derived from the ANOVA table in a straightforward manner. The equations below calculate the variability associated with both the runs and the replicates where the MSwithin represents the “error” or “within-run” mean square, and MSbetween represents the “between-run” mean square.
VarianceRep = MSwithin = 0.102
Click to View Image
[Note—It is common practice to use a value of 0 for VarianceRun when the calculated value is negative. ] Estimates can still be obtained with unequal replication, but the formulas are more complex. Many statistical software packages can easily handle unequal replication. Studying the relative magnitude of the two variance components is important when designing and interpreting a precision study. The insight gained can be used to focus any ongoing method improvement effort and, more important, it can be used to ensure that methods are capable of supporting their intended uses. By carefully defining what constitutes a result (i.e., reportable value), one harnesses the power of averaging to achieve virtually any desired precision. That is, by basing the reportable value on an average across replicates and/or runs, rather than on any single result, one can reduce the %RSD, and reduce it in a predictable fashion.
Table 2 shows the computed variance and %RSD of the mean (i.e., of the reportable value) for different combinations of number of runs and number of replicates per run using the following formulas:
Click to View Image
Click to View Image
Click to View Image
For example, the Variance of the mean, Standard deviation of the mean, and %RSD of a test involving two runs and three replicates per each run are 0.592, 0.769, and 0.76% respectively, as shown below.
Click to View Image
Click to View Image
RSD = (0.769/100.96) × 100% = 0.76%
where 100.96 is the mean for all the data points in Table 1. As illustrated in Table 2, increasing the number of runs from one to two provides a more dramatic reduction in the variability of the reportable value than does increasing the number of replicates per run.
No distributional assumptions were made on the data in Table 1, as the purpose of this Appendix is to illustrate the calculations involved in a precision study.

APPENDIX C: EXAMPLES OF OUTLIER TESTS FOR ANALYTICAL DATA
Given the following set of 10 measurements: 100.0, 100.1, 100.3, 100.0, 99.7, 99.9, 100.2, 99.5, 100.0, and 95.7 (mean = 99.5, standard deviation = 1.369), are there any outliers?
Generalized Extreme Studentized Deviate (ESD) Test
This is a modified version of the ESD Test that allows for testing up to a previously specified number, r, of outliers from a normally distributed population. For the detection of a single outlier (r = 1), the generalized ESD procedure is also known as Grubb's test. Grubb's test is not recommended for the detection of multiple outliers. Let r equal 2, and n equal 10.
Stage 1 (n = 10)— Normalize each result by subtracting the mean from each value and dividing this difference by the standard deviation (see Table 3).4
Take the absolute value of these results, select the maximum value (|R1| = 2.805), and compare it to a previously specified tabled critical value 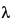1 (2.290) based on the selected significance level (for example, 5%). The maximum value is larger than the tabled value and is identified as being inconsistent with the remaining data. Sources for 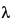-values are included in many statistical textbooks. Caution should be exercised when using any statistical table to ensure that the correct notations (i.e., level of acceptable error) are used when extracting table values.
Stage 2 (n = 9)— Remove the observation corresponding to the maximum absolute normalized result from the original data set, so that n is now 9. Again, find the mean and standard deviation (Table 3, right two columns), normalize each value, and take the absolute value of these results. Find the maximum of the absolute values of the 9 normalized results (|R2| = 1.905), and compare it to 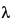2 (2.215). The maximum value is not larger than the tabled value.
Conclusion— The result from the first stage, 95.7, is declared to be an outlier, but the result from the second stage, 99.5, is not an outlier.
Dixon-Type Tests
Dixon's Test can be one-sided or two-sided, depending on an a priori decision as to whether outliers will be considered on one side only. As with the ESD Test, Dixon's Test assumes that the data, in the absence of outliers, come from a single normal population. Following the strategy used for the ESD Test, we proceed as if there were no a priori decision as to side, and so use a two-sided Dixon's Test. From examination of the example data, we see that it is the two smallest that are to be tested as outliers. Dixon provides for testing for two outliers simultaneously; however, these procedures are beyond the scope of this Appendix. The stepwise procedure discussed below is not an exact procedure for testing for the second outlier, because the result of the second test is conditional upon the first. And because the sample size is also reduced in the second stage, the end result is a procedure that usually lacks the sensitivity of Dixon's exact procedures.
Stage 1 (n = 10)— The results are ordered on the basis of their magnitude (i.e., Xn is the largest observation, Xn–1 is the second largest, etc., and X1 is the smallest observation). Dixon's Test has different ratios based on the sample size (in this example, with n = 10), and to declare X1 an outlier, the following ratio, r11, is calculated by the formula:
Click to View Image
A different ratio would be employed if the largest data point was tested as an outlier. The r11 result is compared to an r11, 0.05 value in a table of critical values. If r11 is greater than r11, 0.05, then it is declared an outlier. For the above set of data, r11 = (99.5 – 95.7)/(100.2 – 95.7) = 0.84. This ratio is greater than r11, 0.05, which is 0.52979 at the 5% significance level for a two-sided Dixon's Test. Sources for r11, 0.05 values are included in many statistical textbooks.5
Stage 2— Remove the smallest observation from the original data set, so that n is now 9. The same r11 equation is used, but a new critical r11,0.05 value for n = 9 is needed (r11, 0.05 = 0.56420). Now r11 = (99.7 – 99.5)/(100.2 – 99.5) = 0.29, which is less than r11,0.05 and not significant at the 5% level.
Conclusion— Therefore, 95.7 is declared to be an outlier but 99.5 is not an outlier.
Hampel's Rule
Step 1— The first step in applying Hampel's Rule is to normalize the data. However, instead of subtracting the mean from each data point and dividing the difference by the standard deviation, the median is subtracted from each data value and the resulting differences are divided by MAD (see below). The calculation of MAD is done in three stages. First, the median is subtracted from each data point. Next, the absolute values of the differences are obtained. These are called the absolute deviations. Finally, the median of the absolute deviations is calculated and multiplied by the constant 1.483 to obtain MAD.6
Step 2— The second step is to take the absolute value of the normalized data. Any such result that is greater than 3.5 is declared to be an outlier. Table 4 summarizes the calculations.
The value of 95.7 is again identified as an outlier. This value can then be removed from the data set and Hampel's Rule re-applied to the remaining data. The resulting table is displayed as Table 5. Similar to the previous examples, 99.5 is not considered an outlier.

APPENDIX D: COMPARISON OF METHODS—PRECISION
The following example illustrates the calculation of a 90% confidence interval for the ratio of (true) variances for the purpose of comparing the precision of two methods. It is assumed that the underlying distribution of the sample measurements are well-characterized by normal distributions. For this example, assume the laboratory will accept the alternative method if its precision (as measured by the variance) is no more than four-fold greater than that of the current method.
To determine the appropriate sample size for precision, one possible method involves a trial and error approach using the following formula:
Click to View Image
where n is the smallest sample size required to give the desired power, which is the likelihood of correctly claiming the alternative method has acceptable precision when in fact the two methods have equal precision; 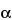is the risk of wrongly claiming the alternative method has acceptable precision; and the 4 is the allowed upper limit for an increase in variance. F-values are found in commonly available tables of critical values of the F-distribution. F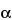,n–1,n–1 is the upper 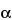percentile of an F-distribution with n – 1 numerator and n – 1 denominator degrees of freedom; that is, the value exceeded with probability 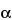. Suppose initially the laboratory guessed a sample size of 11 per method was necessary (10 numerator and denominator degrees of freedom); the power calculation would be as follows:7
Pr [F > ¼F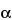,n-1,n-1] = Pr [F > ¼F.05,10,10] = Pr [F > (2.978/4)] = 0.6751
In this case the power was only 68%; that is, even if the two methods had exactly equal variances, with only 11 samples per method, there is only a 68% chance that the experiment will lead to data that permit a conclusion of no more than a four-fold increase in variance. Most commonly, sample size is chosen to have at least 80% power, with choices of 90% power or higher also used. To determine the appropriate sample size, various numbers can be tested until a probability is found that exceeds the acceptable limit (e.g., power >0.90). For example, the power determination for sample sizes of 12–20 are displayed in Table 6. In this case, the initial guess at a sample size of 11 was not adequate for comparing precision, but 15 samples per method would provide a large enough sample size if 80% power were desired, or 20 per method for 90% power.
Typically the sample size for precision comparisons will be larger than for accuracy comparisons. If the sample size for precision is so large as to be impractical for the laboratory to conduct the study, there are some options. The first is to reconsider the choice of an allowable increase in variance. For larger allowable increases in variance, the required sample size for a fixed power will be smaller. Another alternative is to plan an interim analysis at a smaller sample size, with the possibility of proceeding to a larger sample size if needed. In this case, it is strongly advisable to seek professional help from a statistician.
Now, suppose the laboratory opts for 90% power and obtains the results presented in Table 7 based on the data generated from 20 independent runs per method.
Ratio = alternative method variance/current method variance = 45.0/25.0 = 1.8
Lower limit of confidence interval = ratio/F.05 = 1.8/2.168 = 0.83
Upper limit of confidence interval = ratio/F.95 = 1.8/0.461 = 3.90
For this application, a 90% (two-sided) confidence interval is used when a 5% one-sided test is sought. The test is one-sided, because only an increase in standard deviation of the alternative method is of concern. Some care must be exercised in using two-sided intervals in this way, as they must have the property of equal tails—most common intervals have this property. Because the one-side upper confidence limit, 3.90, is less than the allowed limit, 4.0, the study has demonstrated that the alternative method has acceptable precision. If the same results had been obtained from a study with a sample size of 15—as if 80% power had been chosen—the laboratory would not be able to conclude that the alternative method had acceptable precision (upper confidence limit of 4.47).

APPENDIX E: COMPARISON OF METHODS—DETERMINING THE LARGEST ACCEPTABLE DIFFERENCE, , BETWEEN TWO METHODS
This Appendix describes one approach to determining the difference, , between two methods (alternative-current), a difference that, if achieved, still leads to the conclusion of equivalence between the two methods. Without any other prior information to guide the laboratory in the choice of , it is a reasonable way to proceed. Sample size calculations under various scenarios are discussed in this Appendix.
Tolerance Interval Determination
Suppose the process mean and the standard deviation are both unknown, but a sample of size 50 produced a mean and standard deviation of 99.5 and 2.0, respectively. These values were calculated using the last 50 results generated by this specific method for a particular (control) sample. Given this information, the tolerance limits can be calculated by the following formula:
x ± Ks
in which x is the mean; s is the standard deviation; and K is based on the level of confidence, the proportion of results to be captured in the interval, and the sample size, n. Tables providing K values are available. In this example, the value of K required to enclose 95% of the population with 95% confidence for 50 samples is 2.382.8 The tolerance limits are calculated as follows:
99.5 ± 2.382 × 2.0
hence, the tolerance interval is (94.7, 104.3).
Comparison of the Tolerance Limits to the Specification Limits
Assume the specification interval for this method is (90.0, 110.0) and the process mean and standard deviation have not changed since this interval was established. The following quantities can be defined: the lower specification limit (LSL) is 90.0, the upper specification limit (USL) is 110.0, the lower tolerance limit (LTL) is 94.7, and the upper tolerance limit (UTL) is 104.3. Calculate the acceptable difference, (), in the following manner:
A = LTL – LSL for LT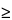L LSL
(A = 94.7 – 90.0 = 4.7);
B = USL – UTL for US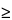L UTL
(B = 110.0 – 104.3 = 5.7); and
= minimum (A, B) = 4.7
Click to View Image
Figure 2. A graph of the quantities calculated above.
With this choice of , and assuming the two methods have comparable precision, the confidence interval for the difference in means between the two methods (alternative-current) should fall within –4.7 and +4.7 to claim that no important difference exists between the two methods.
Quality control analytical laboratories sometimes deal with 99% tolerance limits, in which cases the interval will widen. Using the previous example, the value of K required to enclose 99% of the population with 99% confidence for 50 samples is 3.390. The tolerance limits are calculated as follows:
99.5 ± 3.390 × 2.0
The resultant wider tolerance interval is (92.7, 106.3). Similarly, the new LTL of 92.7 and UTL of 106.3 would produce a smaller :
A = LTL – LSL for LT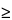L LSL
(A = 92.7 – 90.0 = 2.7);
B = USL – UTL for US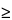L UTL
(B = 110.0 – 106.3 = 3.7); and
= minimum (A, B) = 2.7
Though a manufacturer may choose any that serves adequately in the determination of equivalence, the choice of a larger , while yielding a smaller n, may risk a loss of capacity for discriminating between methods.
Sample Size
Formulas are available that can be used for a specified , under the assumption that the population variances are known and equal, to calculate the number of samples required to be tested per method, n. The level of confidence and power must also be specified. [Note—Power refers to the probability of correctly concluding that two identical methods are equivalent. ] For example, if = 4.7, and the two population variances are assumed to equal 4.0, then, for a 5% level test9 and 80% power (with associated z-values of 1.645 and 1.282, respectively), the sample size is approximated by the following formula:
Click to View Image
Click to View Image
Thus, assuming each method has a population variance, 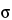2, of 4.0, the number of samples, n, required to conclude with 80% probability that the two methods are equivalent (90% confidence interval for the difference in the true means falls between –4.7 and +4.7) when in fact they are identical (the true mean difference is zero) is 4. Because the normal distribution was used in the above formula, 4 is actually a lower bound on the needed sample size. If feasible, one might want to use a larger sample size. Values for z for common confidence levels are presented in Table 8. The formula above makes three assumptions: 1) the variance used in the sample size calculation is based on a sufficiently large amount of prior data to be treated as known; 2) the prior known variance will be used in the analysis of the new experiment, or the sample size for the new experiment is sufficiently large so that the normal distribution is a good approximation to the t distribution; and 3) the laboratory is confident that there is no actual difference in the means, the most optimistic case. It is not common for all three of these assumptions to hold. The formula above should be treated most often as an initial approximation. Deviations from the three assumptions will lead to a larger required sample size. In general, we recommend seeking assistance from someone familiar with the necessary methods.
When a log transformation is required to achieve normality, the sample size formula needs to be slightly adjusted as shown below. Instead of formulating the problem in terms of the population variance and the largest acceptable difference, , between the two methods, it now is formulated in terms of the population %RSD and the largest acceptable proportional difference between the two methods.
Click to View Image
where
Click to View Image
Click to View Image
and 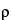represents the largest acceptable proportional difference between the two methods ((alternative-current)/current), and the population %RSDs are assumed known and equal.

APPENDIX F: ADDITIONAL SOURCES OF INFORMATION
There may be a variety of statistical tests that can be used to evaluate any given set of data. This chapter presents several tests for interpreting and managing analytical data, but many other similar tests could also be employed. The chapter simply illustrates the analysis of data using statistically acceptable methods. As mentioned in the Introduction, specific tests are presented for illustrative purposes, and USP does not endorse any of these tests as the sole approach for handling analytical data. Additional information and alternative tests can be found in the references listed below or in many statistical textbooks.
Control Charts:
  1. Manual on Presentation of Data and Control Chart Analysis, 6th ed., American Society for Testing and Materials (ASTM), Philadelphia, 1996.
  2. Grant, E.L., Leavenworth, R.S., Statistical Quality Control, 7th ed., McGraw-Hill, New York, 1996.
  3. Montgomery, D.C., Introduction to Statistical Quality Control, 3rd ed., John Wiley and Sons, New York, 1997.
  4. Ott, E., Schilling, E., Neubauer, D., Process Quality Control: Troubleshooting and Interpretation of Data, 3rd ed., McGraw-Hill, New York, 2000.
Detectable Differences and Sample Size Determination:
  1. CRC Handbook of Tables for Probability and Statistics, 2nd ed., Beyer W.H., ed., CRC Press, Inc., Boca Raton, FL, 1985.
  2. Cohen, J., Statistical Power Analysis for the Behavioral Sciences, 2nd ed., Lawrence Erlbaum Associates, Hillsdale, NJ, 1988.
  3. Diletti, E., Hauschke, D., Steinijans, V.W., “Sample size determination for bioequivalence assessment by means of confidence intervals,” International Journal of Clinical Pharmacology, Therapy and Toxicology, 1991; 29, 1–8.
  4. Fleiss, J.L., The Design and Analysis of Clinical Experiments, John Wiley and Sons, New York, 1986, pp. 369–375.
  5. Juran, J.A., Godfrey, B., Juran's Quality Handbook, 5th ed., McGraw-Hill, 1999, Section 44, Basic Statistical Methods.
  6. Lipsey, M.W., Design Sensitivity Statistical Power for Experimental Research, Sage Publications, Newbury Park, CA, 1990.
  7. Montgomery, D.C., Design and Analysis of Experiments, John Wiley and Sons, New York, 1984.
  8. Natrella, M.G., Experimental Statistics Handbook 91, National Institute of Standards and Technology, Gaithersburg, MD, 1991 (reprinting of original August 1963 text).
  9. Kraemer, H.C., Thiemann, S., How Many Subjects?: Statistical Power Analysis in Research, Sage Publications, Newbury Park, CA, 1987.
  10. van Belle G., Martin, D.C., “Sample size as a function of coefficient of variation and ratio of means,” American Statistician 1993; 47(3): 165–167.
  11. Westlake, W.J., response to Kirkwood, T.B.L.: “Bioequivalence testing—a need to rethink,” Biometrics 1981; 37:589–594.
General Statistics Applied to Pharmaceutical Data:
  1. Bolton, S., Pharmaceutical Statistics: Practical and Clinical Applications, 3rd ed., Marcel Dekker, New York, 1997.
  2. Bolton, S., “Statistics” Remington: The Science and Practice of Pharmacy, 20th ed., Gennaro, A.R., ed., Lippincott Williams and Wilkins, Baltimore, 2000, pp. 124–158.
  3. Buncher, C.R., Tsay, J., Statistics in the Pharmaceutical Industry, Marcel Dekker, New York, 1981.
  4. Natrella, M.G., Experimental Statistics Handbook 91, National Institute of Standards and Technology (NIST), Gaithersburg, MD, 1991 (reprinting of original August 1963 text).
  5. Zar, J., Biostatistical Analysis, 2nd ed., Prentice Hall, Englewood Cliffs, NJ, 1984.
General Statistics Applied to Analytical Laboratory Data:
  1. Gardiner, W.P., Statistical Analysis Methods for Chemists, The Royal Society of Chemistry, London, England, 1997.
  2. Kateman, G., Buydens, L., Quality Control in Analytical Chemistry, 2nd ed., John Wiley and Sons, New York, 1993.
  3. Kenkel, J., A Primer on Quality in the Analytical Laboratory, Lewis Publishers, Boca Raton, FL, 2000.
  4. Mandel, J., Evaluation and Control of Measurements, Marcell Dekker, New York, 1991.
  5. Melveger, A.J., “Statististics in the pharmaceutical analysis laboratory,” Analytical Chemistry in a GMP Environment, Miller J.M., Crowther J.B., eds., John Wiley and Sons, New York, 2000.
  6. Taylor, J.K., Statistical Techniques for Data Analysis, Lewis Publishers, Boca Raton, FL, 1990.
  7. Thode, H.C., Jr., Testing for Normality, Marcel Dekker, New York, NY, 2002.
  8. Taylor, J.K., Quality Assurance of Chemical Measurements, Lewis Publishers, Boca Raton, FL, 1987.
  9. Wernimont, G.T., Use of Statistics to Develop and Evaluate Analytical Methods, Association of Official Analytical Chemists (AOAC), Arlington, VA, 1985.
  10. Youden, W.J., Steiner, E.H., Statistical Manual of the AOAC, AOAC, Arlington, VA, 1975.
Nonparametric Statistics:
  1. Conover, W.J., Practical Nonparametric Statistics, 3rd ed., John Wiley and Sons, New York, 1999.
  2. Gibbons, J.D., Chakraborti, S., Nonparametric Statistical Inference, 3rd ed., Marcel Dekker, New York, 1992.
  3. Hollander, M., Wolfe, D., Nonparametric Statistical Methods, 2nd ed., John Wiley and Sons, NY, 1999.
Outlier Tests:
  1. Barnett, V., Lewis, T., Outliers in Statistical Data, 3rd ed., John Wiley and Sons, New York, 1994.
  2. Böhrer, Armin, “One-sided and Two-sided Critical Values for Dixon's Outlier Test for Sample Sizes up to n = 30,” Economic Quality Control, Vol. 23 (2008), No. 1, pp. 5–13.
  3. Davies, L., Gather, U., “The identification of multiple outliers,” Journal of the American Statistical Association (with comments), 1993; 88:782–801.
  4. Dixon, W.J., “Processing data for outliers,” Biometrics 1953; 9(1):74–89.
  5. Grubbs, F.E., “Procedures for detecting outlying observations in samples,” Technometrics 1969; 11:1–21.
  6. Hampel, F.R., “The breakdown points of the mean combined with some rejection rules,” Technometrics, 1985; 27:95–107.
  7. Hoaglin, D.C., Mosteller, F., Tukey, J., eds., Understanding Robust and Exploratory Data Analysis, John Wiley and Sons, New York, 1983.
  8. Iglewicz B., Hoaglin, D.C., How to Detect and Handle Outliers, American Society for Quality Control Quality Press, Milwaukee, WI, 1993.
  9. Rosner, B., “Percentage points for a generalized ESD many-outlier procedure,” Technometrics, 1983; 25: 165–172.
  10. Standard E-178-94: Standard Practice for Dealing with Outlying Observations, American Society for Testing and Materials (ASTM), West Conshohoken, PA, September 1994.
  11. Rorabacher, D.B., “Statistical Treatment for Rejections of Deviant Values: Critical Values of Dixon's “Q” Parameter and Related Subrange Ratios at the 95% Confidence Level,” Analytical Chemistry, 1991; 63(2): 139–146.
Precision and Components of Variability:
  1. Hicks, C.R., Turner, K.V., Fundamental Concepts in the Design of Experiments, 5th ed., Oxford University Press, 1999 (section on Repeatability and Reproducibility of a Measurement System).
  2. Kirk, R.E., Experimental Design: Procedures for the Behavioral Sciences, Brooks/Cole, Belmont, CA, 1968, pp. 61–63.
  3. Kirkwood, T.B.L., “Geometric means and measures of dispersion,” Letter to the Editor, Biometrics, 1979; 35(4).
  4. Milliken, G.A., Johnson, D.E., Analysis of Messy Data, Volume 1: Designed Experiments, Van Nostrand Reinhold Company, New York, NY, 1984, pp. 19–23.
  5. Searle, S.R., Casella, G., McCulloch, C.E., Variance Components, John Wiley and Sons, New York, 1992.
  6. Snedecor, G.W., Cochran, W.G., Statistical Methods, 8th ed., Iowa State University Press, Ames, IA, 1989.
  7. Standard E-691-87: Practice for Conducting an Interlaboratory Study to Determine the Precision of a Test Method, ASTM, West Conshohoken, PA, 1994.
  8. Hauck, W. W., Koch, W., Abernethy, D., Williams, R. “Making Sense of Trueness, Precision, Accuracy, and Uncertainty,” Pharmacopeial Forum, 2008; 34(3).
Tolerance Interval Determination:
  1. Hahn, G.J., Meeker, W.Q., Statistical Intervals: A Guide for Practitioners, John Wiley and Sons, New York, 1991.
  2. Odeh, R.E., “Tables of two-sided tolerance factors for a normal distribution,” Communications in Statistics: Simulation and Computation, 1978; 7: 183–201.
Table 1. Data from a Precision Study
Replicate
Number		 Run Number
1 2 3 4 5
1 100.70 99.46 99.96 101.80 101.91
2 101.05 99.37 100.17 102.16 102.00
3 101.15 99.59 101.01 102.44 101.67
Mean 100.97 99.47 100.38 102.13 101.86
Standard Deviation 0.236 0.111 0.556 0.321 0.171
% RSD1 0.234% 0.111% 0.554% 0.314% 0.167%
1  %RSD (percent relative standard deviation) = 100% × (standard deviation/mean)
Table 1A. Analysis of Variance Table for Data Presented in Table 1
Source of Variation Degrees of Freedom
(df)		 Sum of Squares
(SS)		 Mean Squares1
(MS)		 F =MSB/MSW
Between Runs 4 14.200 3.550 34.886
Within Runs 10 1.018 0.102  
Total 14 15.217    
1  The Mean Squares Between (MSB) = SSBetween/dfBetween and the Mean Squares Within (MSW) = SSWithin/dfWithin
Table 2. The Predicted Impact of the Test Plan (No. of Runs and No. of Replicates per Run) on the Precision of the Mean
No. of
Runs		 No. of
Replicates per Run		 Variance
of the Mean		 SD of the
Mean		 % RSD1
1 1 1.251 1.118 1.11
1 2 1.200 1.095 1.09
1 3 1.183 1.088 1.08
2 1 0.625 0.791 0.78
2 2 0.600 0.775 0.77
2 3 0.592 0.769 0.76
1  A mean value of 100.96, based on the 15 data points presented in Table 1, was used (as the divisor) to compute the %RSD.
Table 3. Generalized ESD Test Results
  n = 10 n = 9
  Data Normalized Data Normalized
  100.3 +0.555 100.3 +1.361
  100.2 +0.482 100.2 +0.953
  100.1 +0.409 100.1 +0.544
  100.0 +0.336 100.0 +0.136
  100.0 +0.336 100.0 +0.136
  100.0 +0.336 100.0 +0.136
  99.9 +0.263 99.9 –0.272
  99.7 +0.117 99.7 –1.089
  99.5 –0.029 99.5 –1.905
  95.7 –2.805    
Mean = 99.54   99.95  
SD = 1.369   0.245  
Table 4. Test Results Using Hampel's Rule
n = 10
  Data Deviations
from the
Median		 Absolute
Deviations		 Absolute
Normalized
  100.3 0.3 0.3 1.35
  100.2 0.2 0.2 0.90
  100.1 0.1 0.1 0.45
  100 0 0 0
  100 0 0 0
  100 0 0 0
  99.9 –0.1 0.1 0.45
  99.7 –0.3 0.3 1.35
  99.5 –0.5 0.5 2.25
  95.7 –4.3 4.3 19.33
Median = 100   0.15  
MAD =     0.22  
Table 5. Test Results of Re-Applied Hampel's Rule
n = 9
  Data Deviations
from the
Median		 Absolute
Deviations		 Absolute
Normalized
  100.3 0.3 0.3 2.02
  100.2 0.2 0.2 1.35
  100.1 0.1 0.1 0.67
  100 0 0 0
  100 0 0 0
  100 0 0 0
  99.9 –0.1 0.1 0.67
  99.7 –0.3 0.3 2.02
  99.5 –0.5 0.5 3.37
Median = 100   0.1  
MAD =     0.14  
Table 6. Power Determinations for Various Sample Sizes (Specific to the Example in Appendix D)
Sample Size Pr[F >¼ F0.05, n-1, n-1]
12 0.7145
13 0.7495
14 0.7807
15 0.8083
16 0.8327
17 0.8543
18 0.8732
19 0.8899
20 0.9044
Table 7. Example of Measures of Variance for Independent Runs (Specific to the Example in Appendix D)
Method Variance
(standard deviation)		 Sample
Size		 Degrees of
Freedom
Alternative 45.0 (6.71) 20 19
Current 25.0 (5.00) 20 19
Table 8. Common Values for a Standard Normal Distribution
  z-values
Confidence level One-sided () Two-sided (/2)
99% 2.326 2.576
95% 1.645 1.960
90% 1.282 1.645
80% 0.842 1.282
1  Multiple measurements (or, equivalently, the experimental errors associated with the multiple measurements) are independent from one another when they can be assumed to represent a random sample from the population. In such a sample, the magnitude of one measurement is not influenced by, nor does it influence the magnitude of, any other measurement. Lack of independence implies the measurements are correlated over time or space. Consider the example of a 96-well microtiter plate. Suppose that whenever the unknown causes that produce experimental error lead to a low result (negative error) when a sample is placed in the first column and these same causes would also lead to a low result for a sample placed in the second column, then the two resulting measurements would not be statistically independent. One way to avoid such possibilities would be to randomize the placement of the samples on the plate.
2  When data have been log (base e) transformed to achieve normality, the %RSD is:
Click to View Image
This can be reasonably approximated by:
Click to View Image
where s is the standard deviation of the log (base e) transformed data.
3  In general, the sample size required to compare the precision of two methods will be greater than that required to compare the accuracy of the methods.
4  The difference between each value and the mean is termed the residual. Other Studentized residual outlier tests exist where the residual, instead of being divided by the standard deviation, can be divided by the standard deviation times the square root of n –1 divided by n.
5  The critical values for r in this example are taken from Reference 2 under Appendix F, Outlier Tests.
6  Assuming an underlying normal distribution, 1.483 is a constant used so that the resulting MAD is a consistent estimator of the population standard deviation. This means that as the sample size gets larger, MAD gets closer to the population standard deviation.
7  This could be calculated using a computer spreadsheet. For example, in Microsoft® Excel the formula would be: FDIST((R/A)*FINV(alpha, n1, n1), n – 1, n – 1), where R is the ratio of variances at which to determine power (e.g., R = 1, which was the value chosen in the power calculations provided in Table 6) and A is the maximum ratio for acceptance (e.g., A = 4). Alpha is the significance level, typically 0.05.
8  There are existing tables of tolerance factors that give approximate values and thus differ slightly from the values reported here.
9  When testing equivalence, a 5% level test corresponds to a 90% confidence interval.
Auxiliary Information— Please check for your question in the FAQs before contacting USP.
Topic/Question Contact Expert Committee
General Chapter Horacio N. Pappa, Ph.D.
Principal Scientific Liaison
1-301-816-8319		 (STAT2010) Statistics 2010
USP35–NF30 Page 436
Pharmacopeial Forum: Volume No. 36(2) Page 483