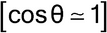941

CHARACTERIZATION OF CRYSTALLINE AND PARTIALLY CRYSTALLINE SOLIDS BY X-RAY POWDER DIFFRACTION (XRPD)

INTRODUCTION

Every crystalline phase of a given substance produces a characteristic X-ray diffraction pattern. Diffraction patterns can be obtained from a randomly oriented crystalline powder composed of crystallites or crystal fragments of finite size. Essentially three types of information can be derived from a powder diffraction pattern: the angular position of diffraction lines (depending on geometry and size of the unit cell), the intensities of diffraction lines (depending mainly on atom type and arrangement, and particle orientation within the sample), and diffraction line profiles (depending on instrumental resolution, crystallite size, strain, and specimen thickness).

Experiments giving angular positions and intensities of lines can be used for applications such as qualitative phase analysis (e.g., identification of crystalline phases) and quantitative phase analysis of crystalline materials. An estimate of the amorphous and crystalline fractions1 can also be made.

The X-ray powder diffraction (XRPD) method provides an advantage over other means of analysis in that it is usually nondestructive in nature (to ensure a randomly oriented sample, specimen preparation is usually limited to grinding). XRPD investigations can also be carried out under in situ conditions on specimens exposed to nonambient conditions such as low or high temperature and humidity.

PRINCIPLES

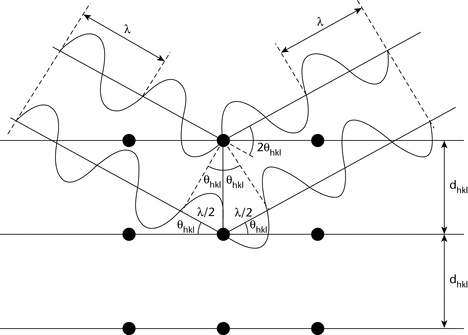
X-ray diffraction results from the interaction between X-rays and electron clouds of atoms. Depending on atomic arrangement, interferences arise from the scattered X-rays. These interferences are constructive when the path difference between two diffracted X-ray waves differs by an integral number of wavelengths. This selective condition is described by the Bragg equation, also called Bragg's law (see Figure 1).

2dhkl sin

hkl = n

Figure 1. Diffraction of X-rays by a crystal according to Bragg's Law.

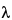
The wavelength,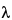

, of the X-rays is of the same order of magnitude as the distance between successive crystal lattice planes, or dhkl (also called d-spacings).

hkl is the angle between the incident ray and the family of lattice planes, and sin

hkl is inversely proportional to the distance between successive crystal planes or d-spacings.

The direction and spacing of the planes with reference to the unit cell axes are defined by the Miller indices {hkl}. These indices are the reciprocals, reduced to the next-lower integer, of the intercepts that a plane makes with the unit cell axes. The unit cell dimensions are given by the spacings a, b, and c, and the angles between them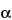

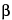, and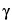

The interplanar spacing for a specified set of parallel hkl planes is denoted by dhkl. Each such family of planes may show higher orders of diffraction where the d values for the related families of planes nh, nk, nl are diminished by the factor 1/n (n being an integer: 2, 3, 4, etc.).

Every set of planes throughout a crystal has a corresponding Bragg diffraction angle,

hkl, associated with it (for a specific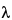

A powder specimen is assumed to be polycrystalline so that at any angle

hkl there are always crystallites in an orientation allowing diffraction according to Bragg's law.2 For a given X-ray wavelength, the positions of the diffraction peaks (also referred to as “lines”, “reflections”, or “Bragg reflections”) are characteristic of the crystal lattice (d-spacings), their theoretical intensities depend on the crystallographic unit cell content (nature and positions of atoms), and the line profiles depend on the perfection and extent of the crystal lattice. Under these conditions, the diffraction peak has a finite intensity arising from atomic arrangement, type of atoms, thermal motion, and structural imperfections, as well as from instrument characteristics.

The intensity is dependent upon many factors such as structure factor, temperature factor, crystallinity, polarization factor, multiplicity, and Lorentz factor.

The main characteristics of diffraction line profiles are 2

position, peak height, peak area, and shape (characterized by, e.g., peak width, or asymmetry, analytical function, and empirical representation). An example of the type of powder patterns obtained for five different solid phases of a substance are shown in Figure 2.

Figure 2. X-ray powder diffraction patterns collected for five different solid phases of a substance (the intensities are normalized).

In addition to the diffraction peaks, an X-ray diffraction experiment also generates a more or less uniform background, upon which the peaks are superimposed. Besides specimen preparation, other factors contribute to the background—for example, sample holder, diffuse scattering from air and equipment, and other instrumental parameters such as detector noise and general radiation from the X-ray tube. The peak-to-background ratio can be increased by minimizing background and by choosing prolonged exposure times.

INSTRUMENT

Instrument Setup

X-ray diffraction experiments are usually performed using powder diffractometers or powder cameras.

A powder diffractometer generally comprises five main parts: an X-ray source; the incident beam optics, which may perform monochromatization, filtering, collimation, and/or focusing of the beam; a goniometer; the diffraction beam optics, which may include monochromatization, filtering, collimation, and focusing or parallelizing of beam; and a detector. Data collection and data processing systems are also required and are generally included in current diffraction measurement equipment.

Depending on the type of analysis to be performed (phase identification, quantitative analysis, lattice parameters determination, etc.), different XRPD instrument configurations and performance levels are required. The simplest instruments used to measure powder patterns are powder cameras. Replacement of photographic film as the detection method by photon detectors has led to the design of diffractometers in which the geometric arrangement of the optics is not truly focusing, but parafocusing, such as in Bragg-Brentano geometry. The Bragg-Brentano parafocusing configuration is currently the most widely used and is therefore briefly described here.

A given instrument may provide a horizontal or vertical

geometry or a vertical

geometry. For both geometries, the incident X-ray beam forms an angle

with the specimen surface plane, and the diffracted X-ray beam forms an angle 2

with the direction of the incident X-ray beam (an angle

with the specimen surface plane). The basic geometric arrangement is represented in Figure 3. The divergent beam of radiation from the X-ray tube (the so-called primary beam) passes through the parallel plate collimators and a divergence slit assembly and illuminates the flat surface of the specimen. All the rays diffracted by suitably oriented crystallites in the specimen at an angle 2

converge to a line at the receiving slit. A second set of parallel plate collimators and a scatter slit may be placed either behind or before the receiving slit. The axes of the line focus and of the receiving slit are at equal distances from the axis of the goniometer. The X-ray quanta are counted by a radiation detector, usually a scintillation counter, a sealed-gas proportional counter, or a position-sensitive solid-state detector such as an imaging plate or CCD detector. The receiving slit assembly and the detector are coupled together and move tangentially to the focusing circle. For

scans, the goniometer rotates the specimen around the same axis as that of the detector, but at half the rotational speed, in a

motion. The surface of the specimen thus remains tangential to the focusing circle. The parallel plate collimator limits the axial divergence of the beam and hence partially controls the shape of the diffracted line profile.

Figure 3. Geometric arrangement of the Bragg-Brentano parafocusing geometry.

A diffractometer may also be used in transmission mode. The advantage with this technology is to lessen the effects due to preferred orientation. A capillary of about 0.5- to 2-mm thickness can also be used for small sample amounts.

X-Ray Radiation

In the laboratory, X-rays are obtained by bombarding a metal anode with electrons emitted by the thermionic effect and accelerated in a strong electric field (using a high-voltage generator). Most of the kinetic energy of the electrons is converted to heat, which limits the power of the tubes and requires efficient anode cooling. A 20- to 30-fold increase in brilliance can be obtained by using rotating anodes and by using X-ray optics. Alternatively, X-ray photons may be produced in a large-scale facility (synchrotron).

The spectrum emitted by an X-ray tube operating at sufficient voltage consists of a continuous background of polychromatic radiation and additional characteristic radiation that depends on the type of anode. Only this characteristic radiation is used in X-ray diffraction experiments. The principal radiation sources used for X-ray diffraction are vacuum tubes using copper, molybdenum, iron, cobalt, or chromium as anodes; copper, molybdenum, or cobalt X-rays are employed most commonly for organic substances (the use of a cobalt anode can especially be preferred to separate distinct X-ray lines). The choice of radiation to be used depends on the absorption characteristics of the specimen and possible fluorescence by atoms present in the specimen. The wavelengths used in powder diffraction generally correspond to the K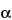

radiation from the anode. Consequently, it is advantageous to make the X-ray beam “monochromatic” by eliminating all the other components of the emission spectrum. This can be partly achieved using K

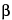filters—that is, metal filters selected as having an absorption edge between the K

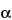and K

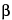wavelengths emitted by the tube. Such a filter is usually inserted between the X-ray tube and the specimen. Another more commonly used way to obtain a monochromatic X-ray beam is via a large monochromator crystal (usually referred to as a “monochromator”). This crystal is placed before or behind the specimen and diffracts the different characteristic peaks of the X-ray beam (i.e., K

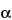and K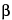

) at different angles so that only one of them may be selected to enter into the detector. It is even possible to separate K

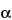1 and K

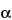2 radiations by using a specialized monochromator. Unfortunately, the gain in getting a monochromatic beam by using a filter or a monochromator is counteracted by a loss in intensity. Another way of separating K

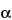and K

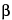wavelengths is by using curved X-ray mirrors that can simultaneously monochromate and focus or parallelize the X-ray beam.

radiation protection

Exposure of any part of the human body to X-rays can be injurious to health. It is therefore essential that whenever X-ray equipment is used, adequate precautions be taken to protect the operator and any other person in the vicinity. Recommended practice for radiation protection as well as limits for the levels of X-radiation exposure are those established by national legislation in each country. If there are no official regulations or recommendations in a country, the latest recommendations of the International Commission on Radiological Protection should be applied.

SPECIMEN PREPARATION AND MOUNTING

The preparation of the powdered material and the mounting of the specimen in a suitable holder are critical steps in many analytical methods, particularly for X-ray powder diffraction analysis, since they can greatly affect the quality of the data to be collected.3 The main sources of errors due to specimen preparation and mounting are briefly discussed in the following section for instruments in Bragg-Brentano parafocusing geometry.

Specimen Preparation

In general, the morphology of many crystalline particles tends to give a specimen that exhibits some degree of preferred orientation in the specimen holder. This is particularly evident for needle-like or platelike crystals when size reduction yields finer needles or platelets. Preferred orientation in the specimen influences the intensities of various reflections so that some are more intense and others less intense, compared to what would be expected from a completely random specimen. Several techniques can be employed to improve randomness in the orientation of crystallites (and therefore to minimize preferred orientation), but further reduction of particle size is often the best and simplest approach. The optimum number of crystallites depends on the diffractometer geometry, the required resolution, and the specimen attenuation of the X-ray beam. In some cases, particle sizes as large as 50 µm will provide satisfactory results in phase identification. However, excessive milling (crystallite sizes less than approximately 0.5 µm) may cause line broadening and significant changes to the sample itself, such as

specimen contamination by particles abraded from the milling instruments (mortar, pestle, balls, etc.),
reduced degree of crystallinity,
solid-state transition to another polymorph,
chemical decomposition,
introduction of internal stress, and
solid-state reactions.

Therefore, it is advisable to compare the diffraction pattern of the nonground specimen with that corresponding to a specimen of smaller particle size (e.g., a milled specimen). If the X-ray powder diffraction pattern obtained is of adequate quality considering its intended use, then grinding may not be required.

It should be noted that if a sample contains more than one phase and if sieving is used to isolate particles to a specific size, the initial composition may be altered.

Specimen Mounting

effect of specimen displacement

A specimen surface that is offset by D with reference to the diffractometer rotation axis causes systematic errors that are very difficult to avoid entirely; for the reflection mode, this results in absolute D·cos

shifts4 in 2

positions (typically of the order of 0.01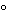

in 2

at low angles

for a displacement D = 15 µm) and asymmetric broadening of the profile toward low 2

values. Use of an appropriate internal standard allows the detection and correction of this effect simultaneously with that arising from specimen transparency. This effect is by far the largest source of errors in data collected on well-aligned diffractometers.

effect of specimen thickness and transparency

When the XRPD method in reflection mode is applied, it is often preferable to work with specimens of “infinite thickness”. To minimize the transparency effect, it is advisable to use a nondiffracting substrate (zero background holder)—for example, a plate of single crystalline silicon cut parallel to the 510 lattice planes.5 One advantage of the transmission mode is that problems with sample height and specimen transparency are less important.

The use of an appropriate internal standard allows the detection and correction of this effect simultaneously with that arising from specimen displacement.

CONTROL OF THE INSTRUMENT PERFORMANCE

The goniometer and the corresponding incident and diffracted X-ray beam optics have many mechanical parts that need adjustment. The degree of alignment or misalignment directly influences the quality of the results of an XRPD investigation. Therefore, the different components of the diffractometer must be carefully adjusted (optical and mechanical systems, etc.) to adequately minimize systematic errors, while optimizing the intensities received by the detector. The search for maximum intensity and maximum resolution is always antagonistic when aligning a diffractometer. Hence, the best compromise must be sought while performing the alignment procedure. There are many different configurations, and each supplier's equipment requires specific alignment procedures. The overall diffractometer performance must be tested and monitored periodically, using suitable certified reference materials. Depending on the type of analysis, other well-defined reference materials may also be employed, although the use of certified reference materials is preferred.

QUALITATIVE PHASE ANALYSIS (IDENTIFICATION OF PHASES)

The identification of the phase composition of an unknown sample by XRPD is usually based on the visual or computer-assisted comparison of a portion of its X-ray powder pattern to the experimental or calculated pattern of a reference material. Ideally, these reference patterns are collected on well-characterized single-phase specimens. This approach makes it possible in most cases to identify a crystalline substance by its 2

-diffraction angles or d-spacings and by its relative intensities. The computer-aided comparison of the diffraction pattern of the unknown sample to the comparison data can be based on either a more or less extended 2

range of the whole diffraction pattern or on a set of reduced data derived from the pattern. For example, the list of d-spacings and normalized intensities, Inorm, a so-called (d, Inorm) list extracted from the pattern, is the crystallographic fingerprint of the material and can be compared to (d, Inorm) lists of single-phase samples compiled in databases.

For most organic crystals, when using Cu K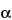

radiation, it is appropriate to record the diffraction pattern in a 2

-range from as near 0

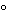as possible to at least 40

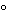. The agreement in the 2

-diffraction angles between specimen and reference is within 0.2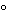

for the same crystal form, while relative intensities between specimen and reference may vary considerably due to preferred orientation effects. By their very nature, variable hydrates and solvates are recognized to have varying unit cell dimensions, and as such, shifting occurs in peak positions of the measured XRPD patterns for these materials. In these unique materials, variance in 2-

positions of greater than 0.2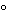

is not unexpected. As such, peak position variances such as 0.2

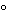are not applicable to these materials. For other types of samples (e.g., inorganic salts), it may be necessary to extend the 2

region scanned to well beyond 40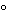

. It is generally sufficient to scan past the 10 strongest reflections identified in single-phase X-ray powder diffraction database files.

It is sometimes difficult or even impossible to identify phases in the following cases:

noncrystallized or amorphous substances,
the components to be identified are present in low mass fractions of the analyte amounts (generally less than 10% m/m),
pronounced preferred orientation effects,
the phase has not been filed in the database used,
the formation of solid solutions,
the presence of disordered structures that alter the unit cell,
the specimen comprises too many phases,
the presence of lattice deformations,
the structural similarity of different phases.

QUANTITATIVE PHASE ANALYSIS

If the sample under investigation is a mixture of two or more known phases, of which not more than one is amorphous, the percentage (by volume or by mass) of each crystalline phase and of the amorphous phase can in many cases be determined. Quantitative phase analysis can be based on the integrated intensities, on the peak heights of several individual diffraction lines,6 or on the full pattern. These integrated intensities, peak heights, or full-pattern data points are compared to the corresponding values of reference materials. These reference materials must be single phase or a mixture of known phases. The difficulties encountered during quantitative analysis are due to specimen preparation (the accuracy and precision of the results require, in particular, homogeneity of all phases and a suitable particle size distribution in each phase) and to matrix effects.

In favorable cases, amounts of crystalline phases as small as 10% may be determined in solid matrices.

Polymorphic Samples

For a sample composed of two polymorphic phases a and b, the following expression may be used to quantify the fraction F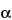

of phase a:

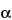= 1/[1 + K(Ib/I

)]

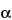The fraction is derived by measuring the intensity ratio between the two phases, knowing the value of the constant K. K is the ratio of the absolute intensities of the two pure polymorphic phases Ioa/Iob. Its value can be determined by measuring standard samples.

Methods Using a Standard

The most commonly used methods for quantitative analysis are

the external standard method,
the internal standard method, and
the spiking method (also often called the standard addition method).

The external standard method is the most general method and consists of comparing the X-ray diffraction pattern of the mixture, or the respective line intensities, with those measured in a reference mixture or with the theoretical intensities of a structural model, if it is fully known.

To limit errors due to matrix effects, an internal reference material can be used that has a crystallite size and X-ray absorption coefficient comparable to those of the components of the sample and with a diffraction pattern that does not overlap at all that of the sample to be analyzed. A known quantity of this reference material is added to the sample to be analyzed and to each of the reference mixtures. Under these conditions, a linear relationship between line intensity and concentration exists. This application, called the internal standard method, requires precise measurement of diffraction intensities.

In the spiking method (or standard addition method), some of the pure phase a is added to the mixture containing the unknown concentration of a. Multiple additions are made to prepare an intensity-versus-concentration plot in which the negative x-intercept is the concentration of the phase a in the original sample.

ESTIMATE OF THE AMORPHOUS AND CRYSTALLINE FRACTIONS

In a mixture of crystalline and amorphous phases, the crystalline and amorphous fractions can be estimated in several ways. The choice of the method used depends on the nature of the sample:

If the sample consists of crystalline fractions and an amorphous fraction of different chemical compositions, the amounts of each of the individual crystalline phases may be estimated using appropriate standard substances, as described above. The amorphous fraction is then deduced indirectly by subtraction.
If the sample consists of one amorphous and one crystalline fraction, either as a 1-phase or a 2-phase mixture, with the same elemental composition, the amount of the crystalline phase (the “degree of crystallinity”) can be estimated by measuring three areas of the diffractogram:

A = total area of the peaks arising from diffraction from the crystalline fraction of the sample,
B = total area below area A,
C = background area (due to air scattering, fluorescence, equipment, etc).

When these areas have been measured, the degree of crystallinity can be roughly estimated as:

% crystallinity = 100A/(A + B – C)

It is noteworthy that this method does not yield an absolute degree of crystallinity values and hence is generally used for comparative purposes only. More sophisticated methods are also available, such as the Ruland method.

SINGLE CRYSTAL STRUCTURE

In general, the determination of crystal structures is performed from X-ray diffraction data obtained using single crystals. However, crystal structure analysis of organic crystals is a challenging task, since the lattice parameters are comparatively large, the symmetry is low, and the scattering properties are normally very low. For any given crystalline form of a substance, the knowledge of the crystal structure allows for calculating the corresponding XRPD pattern, thereby providing a preferred orientation-free reference XRPD pattern, which may be used for phase identification.

1 There are many other applications of the X-ray powder diffraction technique that can be applied to crystalline pharmaceutical substances, such as determination of crystal structures, refinement of crystal structures, determination of the crystallographic purity of crystalline phases, and characterization of crystallographic texture. These applications are not described in this chapter.

2 An ideal powder for diffraction experiments consists of a large number of small, randomly oriented spherical crystallites (coherently diffracting crystalline domains). If this number is sufficiently large, there are always enough crystallites in any diffracting orientation to give reproducible diffraction patterns.

3 Similarly, changes in the specimen can occur during data collection in the case of a nonequilibrium specimen (temperature, humidity).

4 Note that a goniometer zero alignment shift would result in a constant shift on all observed 2

-line positions; in other words, the whole diffraction pattern is, in this case, translated by an offset of Z

in 2

5 In the case of a thin specimen with low attenuation, accurate measurements of line positions can be made with focusing diffractometer configurations in either transmission or reflection geometry. Accurate measurements of line positions on specimens with low attenuation are preferably made using diffractometers with parallel beam optics. This helps to reduce the effects of specimen thickness.

6 If the crystal structures of all components are known, the Rietveld method can be used to quantify them with good accuracy. If the crystal structures of the components are not known, the Pawley method or the partial least-squares (PLS) method can be used.

Auxiliary Information— Please check for your question in the FAQs before contacting USP.

Topic/Question	Contact	Expert Committee
General Chapter	Horacio N. Pappa, Ph.D. Principal Scientific Liaison 1-301-816-8319	(GCCA2010) General Chapters - Chemical Analysis

USP35–NF30 Page 427

Pharmacopeial Forum: Volume No. 35(3) Page 731