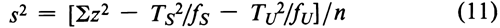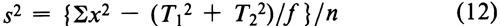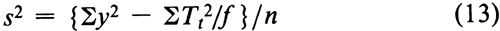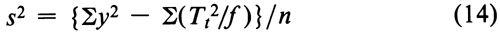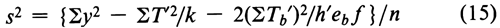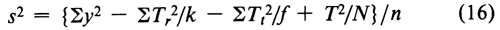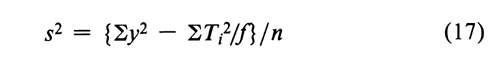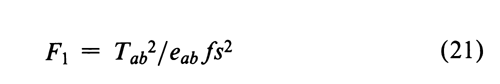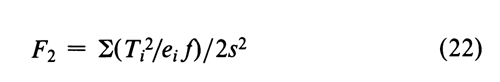Experimental Error and Tests of Assay Validity
As the term is used here, “experimental error” refers to the residual variation in the response of biological indicators, not to a mistake in procedure or to an outlier that needs replacement. It is measured in terms of the error variance of a single response or other unit, which is designated uniformly as s2, despite differences in the definition of the unit. It is required in tests of assay validity and in computing the confidence interval.
Error Variance of a Threshold Dose—
The individual threshold dose is measured directly in some assays. In a Digitalis assay, designate each individual threshold dose by the symbol z, the number or frequency of z's by f, and the total of the z's for each preparation by T, with subscripts S and U for Standard and Unknown, respectively. Compute the error variance of z as
with n = fS + fU  2 degrees of freedom. In the assay of Tubocurarine Chloride Injection, each log-threshold dose of the Unknown is subtracted from the corresponding log-dose of the Standard in the same rabbit to obtain an individual difference x. Since each x may be either positive or negative (+ or
2 degrees of freedom. In the assay of Tubocurarine Chloride Injection, each log-threshold dose of the Unknown is subtracted from the corresponding log-dose of the Standard in the same rabbit to obtain an individual difference x. Since each x may be either positive or negative (+ or 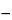 ), it is essential to carry the correct sign in all sums. Designate the total of the x's for the animals injected with the Standard on the first day as T1, and for those injected with the Standard on the second day as T2. Compute the error variance of x with n = N
), it is essential to carry the correct sign in all sums. Designate the total of the x's for the animals injected with the Standard on the first day as T1, and for those injected with the Standard on the second day as T2. Compute the error variance of x with n = N  2 degrees of freedom as
where N is the total number of rabbits that complete the assay, excluding any replacement for a missing value to equalize the size of the two groups.
2 degrees of freedom as
where N is the total number of rabbits that complete the assay, excluding any replacement for a missing value to equalize the size of the two groups.
Error Variance of an Individual Response—
In the Pharmacopeial assays, differences in dose that modify the mean response are assumed not to affect the variability in the response. The calculation of the error variance depends upon the design of the assay and the form of the adjustment for any missing values. Each response is first converted to the unit y used in computing the potency. Determine a single error variance from the combined deviations of the y's around their respective means for each dosage level, summed over all levels. Doubtful values of y may be tested as described under Rejection of Outlying or Aberrant Observations, and proved outliers may be replaced as missing values (see Replacement of Missing Values).
In the simplest design, the units of response are assigned at random to each dosage level, as in the assay for corticotropin. If a missing value is replaced by adding the mean of the remaining y's at any given dosage level to their total, the degrees of freedom (n) in the error variance are reduced by one for each replacement but no other change is needed in the calculation. Assuming that f is then the same for all doses or groups, compute the error variance from the variation within doses of all the y's as
where Tt is the total at each dose of the f values of y, there are k totals Tt and the degrees of freedom n = Sf – k, with Sf diminished by 1 for each replacement.
If variations in f are adjusted by subtracting a group mean from its group total, compute the error variance from the observed y's and the unadjusted totals Tt as
where n = Sf – k.
In the calculation of the result of an assay using the coefficients of Table 6 or 8, s2 may be computed from the response y for each of the h¢ preparations, including the h Unknowns and the corresponding dosage levels of the Standard. For each preparation, compute T¢ = Sy and the slope factor Tb¢ = S(x1y) where the values of x1 are the factorial coefficients for the Standard in the appropriate row b of Table 6 or 8. The error variance for the assay is
where the degrees of freedom n = h¢ (k – 1) – 1, and eb is the ei from the same table and row as the coefficients x1.
The Error Variance in Restricted Designs—
In some assays, the individual responses occur in randomized sets of three or more. Examples of sets are litter mates in the assay of vitamin D, the cleared areas within each plate in an antibiotic assay, and the responses following four successive pairs of injections in the vasopressin assay. Arrange the individual y's from these assays in a 2-way table, in which each column represents a different treatment or dose and each row a randomized set. Losses may be replaced as described under Replacement of Missing Values. The k column totals are the Tt's required for the analysis of balanced designs. The f row totals (Tr) represent a source of variation that does not affect the estimated potency and hence is excluded from the assay error. Compute the approximate error variance from the squares of the individual y's and of the marginal totals as
where T = STr = STt, and the n = (k – 1)(f – 1) degrees of freedom must be diminished by one for any gap in the original table that has been filled by computation.
When the order of treatment is an additional potential source of variation, its effect can be corrected by the dose regimen for a series of n¢ Latin squares with k rows in common, such as that for the two Latin squares in the dose regimens 1 to 4 and 5 to 8 in the assay of Glucagon for Injection. List the observed responses y of each test animal in a separate column in the order of dosing. The responses to each of the k doses then occur equally often in each of the k rows and of the n ¢ k columns, where n¢ is the number of Latin squares. Total the responses y in each row (Tr) in each column (Tc), and, in a separate listing, for each dose or treatment (Tt). An occasional lost reading may be replaced by Equation 1a as described under Replacement of Missing Values. Compute the error variance from the squares of the individual y's and of the marginal and treatment totals as
where T = Sy = STr = STc = STt, N = n ¢ k2, and the n = (k – 1)(n ¢ k – 2) degrees of freedom must be diminished by one for any gap in the original table that has been filled by computation.
In assays where the reactions occur in pairs, the differences between test animals or paired reactions are segregated automatically by calculating the assay with the difference within a pair as the response. With insulin, the response is the difference y in the blood sugar of a single rabbit following two injections (see Insulin Assay  121
121 ). After adjustment for rabbits lost during the assay, compute the error variance of y from the responses in all four groups and from the group totals Ti = T1 to T4 as
). After adjustment for rabbits lost during the assay, compute the error variance of y from the responses in all four groups and from the group totals Ti = T1 to T4 as
where the number of rabbits f is the same in each group and the degrees of freedom, n = 4(f – 1), are reduced by one for each replacement of a rabbit lost during the assay. In the Oxytocin Injection assay, each y represents the difference between the blood pressure response to a dose of the Unknown and the average for the two adjacent doses of Standard. Compute the error variance of y as
with n = 2(f – 1) degrees of freedom, where T1 is the total of the y's for the low dose of the Unknown and T2 that for the high dose.
In a microbial assay calculated by interpolation from a standard curve, convert each difference between two paired responses to units of log-dose, X, by the use of Equation 7. With each difference X as the unit, a composite s2 is computed from the variation in the f values of X for each Unknown, totaled over the h Unknowns in the assay, as
where Tx = SX for a single Unknown and the degrees of freedom n = Sf – h.
Tests of Assay Validity—
In addition to the specific requirements in each monograph and a combined log-dose response curve with a significant slope (see the statistic C in the next section), two conditions determine the validity of an individual factorial assay: (1) the log-dose response curve for the Unknown must parallel that for the Standard within the experimental error, and (2) neither curve may depart significantly from a straight line. When the assay has been completely randomized or consists of randomized sets, the necessary tests are computed with the factorial coefficients for ab, q, and aq from Tables 6 to 8 and the treatment totals Tt. Sum the products of the coefficients in each row by the corresponding Tt's to obtain the product total Ti, where the subscript i stands in turn for ab, q, and aq, respectively. Each of the three ratios, Ti2/ei f, is computed with the corresponding value of ei from the table and with f equal to the number of y's in each Tt. That in row ab tests whether the dosage-response lines are parallel, and is the only test available in a 2-dose assay. With three or more doses of both preparations, that in row q is a test of combined curvature in the same direction, and in row aq of separate curvatures in opposite directions. If any ratio in a 3- or 4-dose assay exceeds s2 as much as three-fold, compute
For a 2-dose assay, compute instead
and for a 3,2 assay (Table 7) determine
For a valid assay, F1, F2, or F3 does not exceed the value given in Table 9 (at odds of 1 in 20) for the degrees of freedom n in s2.
Table 9
| Values of t, t2, F i and |
|||||||||||
| n | t | t2 = F1 | F2 | F3 | n | t | t2 = F1 | F2 | F3 | ||
| 1 | 12.706 | 161.45 | — | — | 3.84 | 19 | 2.093 | 4.381 | 3.52 | 3.13 | 30.1 |
| 2 | 4.303 | 18.51 | 19.00 | 19.16 | 5.99 | 20 | 2.086 | 4.351 | 3.49 | 3.10 | 31.4 |
| 3 | 3.182 | 10.128 | 9.55 | 9.28 | 7.82 | 21 | 2.080 | 4.325 | 3.47 | 3.07 | 32.7 |
| 4 | 2.776 | 7.709 | 6.94 | 6.59 | 9.49 | 22 | 2.074 | 4.301 | 3.44 | 3.05 | 33.9 |
| 5 | 2.571 | 6.608 | 5.79 | 5.41 | 11.07 | 23 | 2.069 | 4.279 | 3.42 | 3.03 | 35.2 |
| 6 | 2.447 | 5.987 | 5.14 | 4.76 | 12.59 | 24 | 2.064 | 4.260 | 3.40 | 3.01 | 36.4 |
| 7 | 2.365 | 5.591 | 4.74 | 4.35 | 14.07 | 25 | 2.060 | 4.242 | 3.38 | 2.99 | 37.7 |
| 8 | 2.306 | 5.318 | 4.46 | 4.07 | 15.51 | 26 | 2.056 | 4.225 | 3.37 | 2.98 | 38.9 |
| 9 | 2.262 | 5.117 | 4.26 | 3.86 | 16.92 | 27 | 2.052 | 4.210 | 3.35 | 2.96 | 40.1 |
| 10 | 2.228 | 4.965 | 4.10 | 3.71 | 18.31 | 28 | 2.048 | 4.196 | 3.34 | 2.95 | 41.3 |
| 11 | 2.201 | 4.844 | 3.98 | 3.59 | 19.68 | 29 | 2.045 | 4.183 | 3.33 | 2.93 | 42.6 |
| 12 | 2.179 | 4.747 | 3.89 | 3.49 | 21.03 | 30 | 2.042 | 4.171 | 3.32 | 2.92 | 43.8 |
| 13 | 2.160 | 4.667 | 3.81 | 3.41 | 22.36 | 40 | 2.021 | 4.085 | 3.23 | 2.84 | 55.8 |
| 14 | 2.145 | 4.600 | 3.74 | 3.34 | 23.68 | 60 | 2.000 | 4.001 | 3.15 | 2.76 | 79.1 |
| 15 | 2.131 | 4.543 | 3.68 | 3.29 | 25.00 | 120 | 1.980 | 3.920 | 3.07 | 2.68 | 146.6 |
| 16 | 2.120 | 4.494 | 3.63 | 3.24 | 26.30 | 1.960 | 3.841 | 3.00 | 2.60 | ||
| 17 | 2.110 | 4.451 | 3.59 | 3.20 | 27.59 | ||||||
| 18 | 2.101 | 4.414 | 3.55 | 3.16 | 28.87 | ||||||
|
†
Adapted from portions of Tables III to V of “Statistical Tables for Biological, Agricultural and Medical Research,” by R. A. Fisher and F. Yates, published by Oliver and Boyd, Ltd., Edinburgh.
|
|||||||||||
An assay may fail the test for validity and still provide a contributory estimate of potency that can be combined profitably with the result of a second assay of the same Unknown, as described in a later section. An end dosage level for either the Standard or the Unknown, or both, may fall outside the linear zone. With three or more dosage levels and relatively large values of Ta, Tab, and Taq, the total response Tt at an end dose of one preparation may approach an upper or lower limit and be responsible for the large values of Tab and Taq. This Tt may be omitted and the assay recomputed with the appropriate design in Table 7. If the assay then meets the test in Equation 20, or 22, the resulting potency, M, may be combined with that of a second assay in computing the log-potency of the Unknown (see under Combination of Independent Assays). If Ta is not significant but Tq shows significant combined curvature, the largest (or smallest) dose of both preparations may be too large (or too small). Their omission may lead to a valid assay with the factorial coefficients for the next smaller design in Table 6 or 8. A statistically significant Tq or STq¢ may be neglected and all dosage levels retained without biasing the computed log-potency M¢ and its confidence interval by more than 5% when the following inequality is true:
where each Tb¢ and Tq¢ is computed with the Tt's (or y's) for a single preparation multiplied by the coefficients for the Standard in rows b and q, respectively. If both Ta and Tab are significant in a 2-dose assay, one Tt may be outside the linear zone. Sometimes a preliminary or contributory estimate of potency can be computed from the remaining three values of Tt and the first design in Table 7. In assays of insulin and of other drugs in which the responses are paired, the test for parallelism is so insensitive that it is omitted. If the tubes in each set are arranged systematically instead of at random in a microbial assay, the tests for validity may be subject to bias from positional effects.