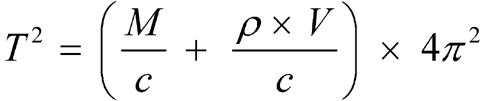Unless otherwise stated in the individual monograph, the specific gravity determination is applicable only to liquids, and, unless otherwise stated, is based on the ratio of the weight of a liquid in air at 25 to that of an equal volume of water at the same temperature. Where a temperature is specified in the individual monograph, the specific gravity is the ratio of the weight of the liquid in air at the specified temperature to that of an equal volume of water at the same temperature. When the substance is a solid at 25
to that of an equal volume of water at the same temperature. Where a temperature is specified in the individual monograph, the specific gravity is the ratio of the weight of the liquid in air at the specified temperature to that of an equal volume of water at the same temperature. When the substance is a solid at 25 , determine the specific gravity of the melted material at the temperature directed in the individual monograph, and refer to water at 25
, determine the specific gravity of the melted material at the temperature directed in the individual monograph, and refer to water at 25 .
.
Unless otherwise stated in the individual monograph, the density is defined as the mass of a unit volume of the substance at 25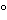 , expressed in kilograms per cubic meter or grams per cubic centimeter (1 kg/m3 = 10–3 g/cm3).
, expressed in kilograms per cubic meter or grams per cubic centimeter (1 kg/m3 = 10–3 g/cm3).
Unless otherwise directed in the individual monograph, use Method I.
METHOD I
Procedure—
Select a scrupulously clean, dry pycnometer that previously has been calibrated by determining its weight and the weight of recently boiled water contained in it at 25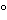 . Adjust the temperature of the liquid to about 20
. Adjust the temperature of the liquid to about 20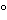 , and fill the pycnometer with it. Adjust the temperature of the filled pycnometer to 25
, and fill the pycnometer with it. Adjust the temperature of the filled pycnometer to 25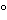 , remove any excess liquid, and weigh. When the monograph specifies a temperature different from 25
, remove any excess liquid, and weigh. When the monograph specifies a temperature different from 25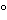 , filled pycnometers must be brought to the temperature of the balance before they are weighed. Subtract the tare weight of the pycnometer from the filled weight.
, filled pycnometers must be brought to the temperature of the balance before they are weighed. Subtract the tare weight of the pycnometer from the filled weight.
The specific gravity of the liquid is the quotient obtained by dividing the weight of the liquid contained in the pycnometer by the weight of water contained in it, both determined at 25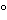 , unless otherwise directed in the individual monograph.
, unless otherwise directed in the individual monograph.
METHOD II
The procedure includes the use of the Oscillating transducer density meter. The apparatus consists of the following:
- a U-shaped tube, usually of borosilicate glass, which contains the liquid to be examined;
- a magneto-electrical or piezo-electrical excitation system that causes the tube to oscillate as a cantilever oscillator at a characteristic frequency depending on the density of the liquid to be examined;
- a means of measuring the oscillation period (T), which may be converted by the apparatus to give a direct reading of density or used to calculate density by using the constants A and B described below; and
- a means to measure and/or control the temperature of the oscillating transducer containing the liquid to be tested.
The oscillation period is a function of the spring constant (c) and the mass of the system:
where 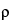 is the density of the liquid to be tested, M is the mass of the tube, and V is the volume of the filled tube.
is the density of the liquid to be tested, M is the mass of the tube, and V is the volume of the filled tube.
Introduction of two constants A = c / (4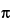 2 × V) and B = M / V, leads to the classical equation for the oscillating transducer:
2 × V) and B = M / V, leads to the classical equation for the oscillating transducer:
The specific gravity of the liquid is given by the formula:
where 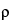 (L) and
(L) and 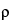 (W) are the densities of the liquid and water, respectively, both determined at 25
(W) are the densities of the liquid and water, respectively, both determined at 25 , unless otherwise directed in the individual monograph.
, unless otherwise directed in the individual monograph.
Calibration—
The constants A and B are determined by operating the instrument with the U-tube filled with two different samples of known density (e.g., degassed water and air). Perform the control measurements daily, using degassed water: the results displayed for the control measurement using degassed water do not deviate from the reference value (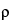 25 = 0.997043 g/cm–3) by more than its specified error. Precision is a function of the repeatability and stability of the oscillator frequency. Density meters are able to achieve measurements with an error on the order of 1×10–3g/cm–3 to 1×10–5g/cm–3 and a repeatability of 1×10–4g/cm–3 to 1×10–6g/cm–3. For example, an instrument specified to ±1×10–4g/cm–3 must display 0.9970 ± 0.0001 g/cm–3 in order to be suitable for further measurement, otherwise a readjustment is necessary. Calibration with certified reference materials should be carried out regularly.
25 = 0.997043 g/cm–3) by more than its specified error. Precision is a function of the repeatability and stability of the oscillator frequency. Density meters are able to achieve measurements with an error on the order of 1×10–3g/cm–3 to 1×10–5g/cm–3 and a repeatability of 1×10–4g/cm–3 to 1×10–6g/cm–3. For example, an instrument specified to ±1×10–4g/cm–3 must display 0.9970 ± 0.0001 g/cm–3 in order to be suitable for further measurement, otherwise a readjustment is necessary. Calibration with certified reference materials should be carried out regularly.
Procedure—
Using the manufacturer's instructions, perform the measurements using the same procedure as for Calibration. If necessary, equilibrate the liquid to be examined at 25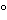 before introduction into the tube to avoid the formation of bubbles and to reduce the time required for measurement. Factors affecting accuracy include the following:
before introduction into the tube to avoid the formation of bubbles and to reduce the time required for measurement. Factors affecting accuracy include the following:
- temperature uniformity throughout the tube,
- nonlinearity over a range of density,
- parasitic resonant effects, and
- viscosity, if the oscillating transducer density meters used do not provide automatic compensation of sample viscosity influence.
Auxiliary Information— Please check for your question in the FAQs before contacting USP.
| Topic/Question | Contact | Expert Committee |
| General Chapter | Gary E. Ritchie, M.Sc.
Scientific Fellow 1-301-816-8353 |
(GC05) General Chapters 05 |
USP32–NF27 Page 369
Pharmacopeial Forum: Volume No. 31(2) Page 515